(Sin diferencias)
| |
Última revisión de 15:37 19 mar 2018
Al abordar los problemas ontológicos de la Mecánica Cuántica (MC), resulta conveniente comenzar con algunas consideraciones preliminares. En primer lugar, el concepto de problema es relativo: algunos tópicos o situaciones podrían ser considerados problemáticos desde un punto de vista, pero podrían pasar inadvertidos desde otro. Cuando hablemos de problemas ontológicos de la mecánica cuántica nos referiremos a aquellos resultados o situaciones donde los objetos cuánticos no se comportan como esperaríamos que lo hiciesen de acuerdo con nuestra manera usual (clásica) de pensar y considerar los fenómenos físicos; o, dicho de otra manera, donde nuestras convicciones cotidianas e intuiciones ontológicas son puestas en jaque y resultan incapaces de dar cuenta del fenómeno considerado de una manera coherente y unificada. Probablemente, si fuésemos seres vivientes y pensantes del tamaño de la escala de Planck, no encontraríamos esta clase de problemas (aunque quizás encontraríamos otros): pensaríamos que los sistemas físicos simplemente se comportan como se supone que deben comportarse de acuerdo con las leyes que rigen en su ámbito; más aún, quizás nos consternaría que los objetos de gran escala se comportaran de una manera extraña, evadiendo el principio de superposición o el principio de incerteza. Por lo tanto, lo que aquí consideraremos como problemas ontológicos encontrarán su contrapunto en ejemplos clásicos: este comportamiento cuántico es problemático porque, usualmente, a nuestra escala, las cosas se comportan de manera muy distinta.
En segundo lugar, nos ceñiremos a problemas de naturaleza exclusivamente ontológica. La mecánica cuántica nos provee de un repertorio muy variado de situaciones que pueden resultar conflictivas desde un punto de vista formal, físico, epistémico o incluso teológico. En este trabajo no intentaremos cubrir todos estos matices. Al referirnos a problemas ontológicos nos referimos a problemas ligados a qué entidades, propiedades y relaciones hay en el mundo de acuerdo con la mecánica cuántica. O, en otras palabras, qué descripción del mundo nos ofrece la mecánica cuántica. En filosofía general de las ciencias existe un famoso y extendido debate acerca de cómo interpretar las entidades teóricas (y las leyes) que una teoría científica postula. Tales entidades, ¿son objetos reales que están en el mundo –aunque sean inobservables? ¿O son meros instrumentos conceptuales o formales que no tienen referencia alguna? Esta entrada asumirá, desde el principio, un enfoque realista de las entidades que la mecánica cuántica postula, y esto por obvias razones: técnicamente, no hay ningún genuino problema ontológico en la mecánica cuántica si, a priori, se considera que las entidades acerca de las cuales la teoría habla no existen. Muchos de estos problemas, claramente, se disolverían automáticamente si la mecánica cuántica fuese un mero aparato formal capaz de ofrecer precisas y exitosas predicciones, pero sin referir a nada en el mundo, sin la capacidad de informarnos acerca de cómo es el mundo si la teoría fuese verdadera.
Por lo tanto, esta entrada buscará marcar y exponer algunos de los puntos donde nuestras intuiciones clásicas -respecto de cómo se comportan los objetos físicos del mundo, qué es un estado físico, cómo son las propiedades de un sistema y cómo se pueden determinar, qué tipo de relaciones existen en el mundo entre objetos físicos etc.- entran en conflicto con la manera en la que sistemas cuánticos, tales como fotones y electrones, se describen y se comportan de acuerdo con la mecánica cuántica.
Contenido
- 1 Nociones formales y principios básicos
- 2 Formalismo y realidad
- 3 Propiedades posibles de un sistema cuántico: el principio de superposición
- 4 ¿Límite ontológico o mera ignorancia? Incerteza y contextualidad
- 5 ¿Hay realidad más allá de medir? El problema de la medición
- 6 ¿Hay objetos cuánticos? El problema de la individualidad de las partículas
- 7 Comentarios finales
- 8 Bibliografía
- 9 Cómo Citar
- 10 Derechos de autor
- 11 Herramientas académicas
- 12 Agradecimientos
1 Nociones formales y principios básicos ↑
Esta primera sección se propone ofrecer algunas herramientas formales básicas que faciliten al lector comprender algunos de los problemas que serán abordados a lo largo de la entrada. Para ello, se definirán formalmente, y a manera de resumen, nociones tales como las de estado cuántico, observable y otros conceptos sobre los cuales volveremos una y otra vez al tratar los diversos problemas ontológicos en las secciones subsiguientes. Para una exposición mucho más detallada y completa del aparato formal, puede consultarse cualquier manual de mecánica cuántica (Ballentine 1998, Shankar 1994) o, si se prefiere bibliografía de carácter más introductorio y explicativo que, sin dejar de lado aspectos formales, permite una discusión más orientada a los fundamentos conceptuales de la teoría, pueden consultarse los siguientes libros: The Structure and Interpretation of Quantum Mechanics (Hughes 1989), Quantum Reality (Allday 2009) y Quantum Mechanics: the Theoretical Minimum (Susskind y Friedman 2014).
El nacimiento y desarrollo de la mecánica cuántica no fue producto de una empresa o trabajo personal. A diferencia de los Principia Mathematica de Newton (1687), por ejemplo, no existe nada así como un corpus teórico fundacional que establezca los rasgos fundamentales de la teoría. Por el contrario, la “Antigua Teoría Cuántica” (“Old Quantum Mechanics”, como se denomina a la teoría forjada durante su periodo fundacional) fue el resultado del esfuerzo de numerosos científicos durante el primer cuarto del siglo XX, en la búsqueda de una comprensión sistemática y precisa de nuevos resultados teóricos y experimentales que contradecían toda la física existente hasta esos días (la mecánica newtoniana, la mecánica estadística clásica, el electromagnetismo maxwelliano y la termodinámica). Talentosos científicos y filósofos como Niels Bohr, Albert Einstein, Max Planck, Wolfgang Pauli, Werner Heisenberg y Erwin Schrödinger, entre otros, hicieron sus significativos aportes para, ladrillo a ladrillo, ir construyendo el formalismo de la teoría cuántica, al menos en su primera versión. En esta entrada utilizaremos un enfoque más actualizado, formulado en espacios de Hilbert. Consideramos que esta es la manera más efectiva en vistas a entender algunos conceptos básicos y poder tratar los problemas filosóficos que se irán presentando.
Los estados de un sistema cuántico son representados en un espacio de Hilbert ![]() , que es un espacio vectorial lineal complejo, es decir, es un conjunto de vectores cerrado bajo la suma y la multiplicación por escalares que pertenecen al campo de los números complejos. Para cada instante, el estado del sistema cuántico es representado por un único vector
, que es un espacio vectorial lineal complejo, es decir, es un conjunto de vectores cerrado bajo la suma y la multiplicación por escalares que pertenecen al campo de los números complejos. Para cada instante, el estado del sistema cuántico es representado por un único vector ![]() (ket, en notación de Dirac) en un espacio de Hilbert:
(ket, en notación de Dirac) en un espacio de Hilbert: ![]() ∈
∈![]() .
.
Por otra parte, las propiedades de un sistema cuántico, llamadas en física observables, se representan mediante operadores sobre el espacio de Hilbert. Matemáticamente, un observable ![]() se representa mediante un operador
se representa mediante un operador ![]() que tiene autovectores
que tiene autovectores ![]() y autovalores
y autovalores ![]() , de manera que si se multiplica un autovector por el operador, el resultado es una constante (el autovalor) por el autovector original, es decir,
, de manera que si se multiplica un autovector por el operador, el resultado es una constante (el autovalor) por el autovector original, es decir, ![]() .
.
Desde el punto de vista físico, los autovalores ![]() del operador
del operador ![]() son los valores que es posible obtener en una medición de la propiedad
son los valores que es posible obtener en una medición de la propiedad ![]() . Para calcular magnitudes de interés físico, se realizan operaciones algebraicas a partir de los mencionados operadores. Así, por ejemplo, el valor medio de la propiedad representada por
. Para calcular magnitudes de interés físico, se realizan operaciones algebraicas a partir de los mencionados operadores. Así, por ejemplo, el valor medio de la propiedad representada por ![]() , para un sistema en el estado
, para un sistema en el estado ![]() , se calcula como
, se calcula como ![]() . Estos valores medios son resultados que pueden calcularse directamente a partir de los datos obtenidos en los experimentos.
. Estos valores medios son resultados que pueden calcularse directamente a partir de los datos obtenidos en los experimentos.
Vale la pena agregar que los operadores que se utilizan en mecánica cuántica tienen todos sus autovalores reales y sus autovectores son ortogonales (cf., i.e., Ballentine 1998). Por lo tanto, los autovectores de un operador que representa un observable cuántico pueden formar una base del espacio de Hilbert (y, de hecho, así sucede cuando el operador es no degenerado, cf. Ballentine 1998). Una base para los estados es un conjunto de vectores a partir de los cuales, por medio de una combinación lineal, es posible expresar cualquier vector de estado. Por ejemplo, si los estados ![]() forman una base del espacio de Hilbert
forman una base del espacio de Hilbert ![]() de dimensión
de dimensión ![]() , entonces cualquier vector de estado
, entonces cualquier vector de estado ![]() se puede escribir como
se puede escribir como
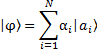
donde los coeficientes ![]() son números complejos. Puesto que hay infinitas bases del espacio de Hilbert
son números complejos. Puesto que hay infinitas bases del espacio de Hilbert ![]() , el mismo vector
, el mismo vector ![]() se puede representar en la base
se puede representar en la base ![]() , de manera que
, de manera que
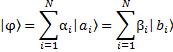
donde los coeficientes ![]() también son números complejos, los cuales mantienen una relación con los coeficientes
también son números complejos, los cuales mantienen una relación con los coeficientes ![]() que depende de cuáles sean los vectores de cada base.
que depende de cuáles sean los vectores de cada base.
Para ilustrar estos conceptos, presentemos un ejemplo. Consideremos un sistema cuántico que se encuentra en un estado representado por el vector ![]() , y un observable
, y un observable ![]() representado por el operador
representado por el operador ![]() con autovectores
con autovectores ![]() y
y ![]() , que forman una base de un espacio de Hilbert de dos dimensiones. El vector
, que forman una base de un espacio de Hilbert de dos dimensiones. El vector ![]() puede representarse como una combinación lineal de los estados de la base, con coeficientes
puede representarse como una combinación lineal de los estados de la base, con coeficientes ![]() y
y ![]() (Figura 1.1):
(Figura 1.1):
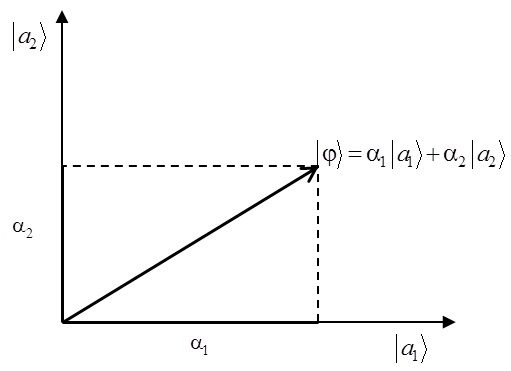
De acuerdo con la regla de Born, los coeficientes elevados al cuadrado, ![]() y
y ![]() , miden las probabilidades de que el observable adquiera los valores
, miden las probabilidades de que el observable adquiera los valores ![]() y
y ![]() , respectivamente, cuando el sistema se encuentra en el estado representado por el vector
, respectivamente, cuando el sistema se encuentra en el estado representado por el vector ![]() (obsérvese que, de acuerdo con el teorema de Pitágoras,
(obsérvese que, de acuerdo con el teorema de Pitágoras, ![]() , tal como debe suceder con la suma de las probabilidades de todos los casos posibles).
, tal como debe suceder con la suma de las probabilidades de todos los casos posibles).
La evolución del estado a lo largo del tiempo se rige por la ecuación de Schrödinger, que constituye el postulado dinámico de la teoría. De esta manera, un estado inicial ![]() se convierte en
se convierte en ![]() :
:
donde ![]() es el operador hamiltoniano del sistema, esto es, el operador que corresponde al observable energía.
es el operador hamiltoniano del sistema, esto es, el operador que corresponde al observable energía.
La representación en términos de vectores de estado es apropiada en muchos casos, pero no es la más general. Con el vector de estado ![]() es posible construir el operador de estado
es posible construir el operador de estado ![]() (representado usualmente mediante una matriz densidad) del siguiente modo:
(representado usualmente mediante una matriz densidad) del siguiente modo:
La representación matemática del operador de estado se realiza en el espacio de Liouville ![]() , que es el producto tensorial del espacio de Hilbert por sí mismo:
, que es el producto tensorial del espacio de Hilbert por sí mismo: ![]() , siendo
, siendo ![]() un espacio “más grande” que el espacio de Hilbert. Por lo tanto, el espacio de Liouville permite la representación de estados que no existen en el espacio de Hilbert y, por ello, brinda una representación más general que la representación tradicional en un espacio de Hilbert. La evolución del operador de estado viene dada por la ecuación de Schrödinger en versión de von Neumann:
un espacio “más grande” que el espacio de Hilbert. Por lo tanto, el espacio de Liouville permite la representación de estados que no existen en el espacio de Hilbert y, por ello, brinda una representación más general que la representación tradicional en un espacio de Hilbert. La evolución del operador de estado viene dada por la ecuación de Schrödinger en versión de von Neumann:
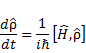
donde, nuevamente, ![]() es el hamiltoniano del sistema, y el conmutador
es el hamiltoniano del sistema, y el conmutador ![]() se calcula como
se calcula como ![]() .
.
El formalismo de la mecánica cuántica también permite describir y dar cuenta de la evolución de sistemas compuestos, es decir, sistemas donde interviene más de una partícula. En el caso de sistemas compuestos, el estado inicial del sistema total se construye como el producto tensorial de los estados de sus subsistemas del siguiente modo (Landau y Lifshitz 1972):
- Se consideran dos partículas inicialmente separadas e independientes: la partícula 1 en el estado
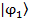 y la partícula 2 en el estado
y la partícula 2 en el estado 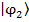 .
.
- Se asume que, a partir del instante
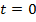 las dos partículas serán consideradas partes de un sistema compuesto total cuyo estado inicial es
las dos partículas serán consideradas partes de un sistema compuesto total cuyo estado inicial es 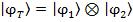 .
.
2 Formalismo y realidad ↑
Hasta aquí hemos presentado algunos rasgos generales del formalismo de la mecánica cuántica que permitirán al lector seguir con relativa facilidad los problemas ontológicos que iremos presentando a lo largo del texto. Cabe aclarar que, en tanto aparato formal capaz de hacer predicciones, la mecánica cuántica es una teoría sumamente exitosa en su campo de aplicación: su gran precisión predictiva y los numerosos logros tecnológicos a los que ha dado lugar están fuera de cualquier discusión. Sin embargo, una teoría científica no es meramente un aparato formal capaz de hacer predicciones, totalmente desvinculado de la realidad: contiene afirmaciones acerca de cómo es el mundo o de cuál es el entretejido que constituye la realidad (sus entidades, sus propiedades, sus leyes) de acuerdo a la teoría.
Al considerar este segundo aspecto de cualquier teoría científica, inescindible del primero, la mecánica cuántica ha dado lugar a una enorme discusión que ha concentrado el esfuerzo de numerosos físicos y filósofos desde el nacimiento mismo de la teoría a principios del siglo XX. Hasta el momento, no existe consenso alguno acerca de cómo es el mundo de acuerdo a la mecánica cuántica. Por el contrario, una plétora de interpretaciones se ha abierto paso, conquistando hegemonías temporales y geográficas. Cada interpretación ha buscado elaborar un marco conceptual coherente y sistemático capaz de dotar de sentido epistémico y ontológico al aparato formal tan exitoso; sin embargo ninguna ha logrado sortear todos los problemas que la teoría presenta a la hora de lograr tal sistematización y coherencia conceptual. Es por ello mismo que la discusión acerca de los problemas ontológicos de la mecánica cuántica aún cobra pleno sentido.
A continuación detallaremos algunos de estos problemas ontológicos que se han debatido a lo largo de la ya larga historia de la teoría. La lista no puede ser exhaustiva ya que la propia selección de problemas es objeto discusión. Sin embargo, consideramos que la selección que aquí se presentará cubre un rango aceptable, permitiendo obtener no sólo un amplio panorama de la cuestión sino también un muestreo de los problemas más discutidos en la actualidad. Tampoco es nuestra intención exponer todas las propuestas formuladas en vistas a solución a cada problema presentado: tales tópicos, con sus argumentos y contra-argumentos, se pueden encontrar de manera más completa y precisa en algunas entradas de esta misma Enciclopedia o en otras (v.g. Stanford Encyclopedia of Philosophy disponible online), a las cuales referiremos oportunamente. Naturalmente, muchos de los problemas que se mencionarán están tan estrechamente relacionados que aparecerán una y otra vez en distintos puntos, al mencionar diferentes características o principios de la mecánica cuántica. La idea central de esta entrada consiste en brindar un mapa general acerca de los principales problemas ontológicos de la mecánica cuántica, con sus aspectos más relevantes, y las referencias pertinentes para una ulterior profundización sobre el tema.
3 Propiedades posibles de un sistema cuántico: el principio de superposición ↑
Un buen punto de partida para comenzar a considerar los problemas ontológicos vinculados con la mecánica cuántica es el principio de superposición. Este principio constituye uno de los fundamentos de la teoría y uno de los primeros puntos de divergencia respecto de la física clásica. Paul Dirac (1967 [1930]) sostenía que “[el principio de superposición] da forma a la nueva y fundamental idea de la mecánica cuántica y las bases de la divergencia respecto de la teoría clásica” (1967, 2). Párrafos después, enfatiza: “Es importante recordar (…) que la superposición que ocurre en mecánica cuántica es de una naturaleza esencialmente diferente de cualquiera que ocurre en la teoría clásica” (1967, 14). Pero, ¿qué dice el principio de superposición? ¿Cuál es su contenido físico y cuáles son sus implicancias ontológicas?
En mecánica clásica (y también de acuerdo a nuestras intuiciones cotidianas), a la hora de pensar una propiedad de un objeto determinado (fundamentalmente una propiedad intrínseca, es decir, una propiedad que el objeto posee en sí mismo sin relación a ningún elemento externo o contexto), como por ejemplo la propiedad de “tener carga negativa”, consideramos que el objeto cumple o no cumple con la propiedad, la propiedad es o no es instanciada por el objeto. No sostendríamos con sentido que el objeto posee y no posee la propiedad de “tener carga negativa” de manera simultánea: non tertium datur. En general, creemos, un sistema tiene o no tiene cierta masa, tiene o no tiene cierto valor de energía, está o no está en cierta posición, etc. Para expresar la idea en el mismo lenguaje que el introducido en la sección anterior, consideremos un objeto que se comporta de acuerdo con las leyes de la física clásica: un sistema ![]() del cual es posible medir una propiedad
del cual es posible medir una propiedad ![]() , la cual posee un conjunto de valores posibles
, la cual posee un conjunto de valores posibles ![]() . Supongamos, como usualmente se admite, que si el sistema tiene la propiedad “tener el valor
. Supongamos, como usualmente se admite, que si el sistema tiene la propiedad “tener el valor ![]() ”, entonces se encuentra en el estado
”, entonces se encuentra en el estado ![]() . Por lo tanto, la propiedad
. Por lo tanto, la propiedad ![]() tiene un operador asociado
tiene un operador asociado ![]() , y el conjunto
, y el conjunto ![]() es el conjunto de sus autovalores (es decir, los posibles valores que la propiedad puede adquirir). El rasgo fundamental de la física clásica es que el sistema en cuestión sólo tendrá estados con valores definidos: o bien se encuentra en el estado
es el conjunto de sus autovalores (es decir, los posibles valores que la propiedad puede adquirir). El rasgo fundamental de la física clásica es que el sistema en cuestión sólo tendrá estados con valores definidos: o bien se encuentra en el estado ![]() con valor
con valor ![]() de la propiedad
de la propiedad ![]() , o bien se encuentra en el estado
, o bien se encuentra en el estado ![]() con valor
con valor ![]() , o bien en cualquier otro estado de los posibles. En otras palabras, los únicos estados posibles de un sistema clásico son los autoestados de
, o bien en cualquier otro estado de los posibles. En otras palabras, los únicos estados posibles de un sistema clásico son los autoestados de ![]() ,
, ![]() .
.
El principio de superposición entra en juego a la hora de pensar cuáles son los estados posibles de un sistema cuántico. Mientras que en el caso clásico, como dijimos, los únicos estados posibles son los autoestados de un observable determinado, la teoría cuántica contempla otro tipo de estados. En términos generales, el principio de superposición afirma que cualquier combinación lineal de autoestados también es un estado posible del sistema. Volviendo al ejemplo anterior, pero ahora considerando que ![]() es un sistema cuántico,
es un sistema cuántico, ![]() podría encontrarse en cualquiera de los autoestados
podría encontrarse en cualquiera de los autoestados ![]() de
de ![]() . Pero también podría encontrarse en un estado
. Pero también podría encontrarse en un estado ![]() que fuera una superposición de los autoestados de
que fuera una superposición de los autoestados de ![]() , siendo esta superposición un estado genuino del sistema:
, siendo esta superposición un estado genuino del sistema:
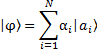
Tomando el caso sencillo de un observable con dos autoestados, por ejemplo una imaginaria “moneda cuántica” con los estados ![]() y
y ![]() ,
, ![]() podría ser o bien el estado
podría ser o bien el estado ![]() , o bien el estado
, o bien el estado ![]() , o bien una combinación lineal de ellos:
, o bien una combinación lineal de ellos:
donde ![]() y
y ![]() son números complejos, cuyos módulos al cuadrado,
son números complejos, cuyos módulos al cuadrado, ![]() y
y ![]() , indican la probabilidad de que la moneda adquiera la propiedad “cara hacia arriba” y “cruz hacia arriba” respectivamente. Es importante señalar (y es uno de las primeras curiosidades o particularidades de la mecánica cuántica) que el estado
, indican la probabilidad de que la moneda adquiera la propiedad “cara hacia arriba” y “cruz hacia arriba” respectivamente. Es importante señalar (y es uno de las primeras curiosidades o particularidades de la mecánica cuántica) que el estado ![]() no es ni cara ni cruz, y no es reductible a ninguno de ellos. El principio de superposición parece vaciar de sentido la pregunta “la moneda (cuántica), ¿está realmente cara hacia arriba o cara hacia abajo?”, que sólo contempla la posibilidad de dos estados excluyentes. El principio parece forzarnos a considerar la existencia de un tipo particular (y desconcertante) de estados, las superposiciones.
no es ni cara ni cruz, y no es reductible a ninguno de ellos. El principio de superposición parece vaciar de sentido la pregunta “la moneda (cuántica), ¿está realmente cara hacia arriba o cara hacia abajo?”, que sólo contempla la posibilidad de dos estados excluyentes. El principio parece forzarnos a considerar la existencia de un tipo particular (y desconcertante) de estados, las superposiciones.
Naturalmente, la posibilidad de superposiciones, resultado del principio de superposición, despiertan una serie de interrogantes remarcables. El propio Dirac consideraba que la existencia de estos estados era un enigma central de la mecánica cuántica. De manera general, pueden identificarse dos problemas centrales. En primer lugar, si bien la existencia de los estados superpuestos es una consecuencia directa e incuestionable del formalismo de la mecánica cuántica, ¿por qué nunca observamos superposiciones? Cada vez que un experimento es llevado a cabo, sólo observamos y registramos valores definidos de los observables del sistema a medir: ¿por qué esto sucede de esta manera? Sin embargo, si la mecánica cuántica es una fiel descripción de la realidad microscópica, la superposición es un aspecto fundamental del mundo. Más aún, los estados “naturales” de los sistemas cuánticos, siempre y cuando no sean observados, son superposiciones de los autoestados de alguno de sus observables: ¿debemos aceptar dichos estados de superposición como parte de la realidad más allá de ser empíricamente inaccesibles y retar nuestras teorías clásicas acerca de sistemas físicos y sus estados posibles? Esta serie de preguntas volverán a surgir cuando presentemos y abordemos un famoso problema en mecánica cuántica, el problema de la medición.
En segundo lugar, aceptada la existencia de las superposiciones, ¿qué es ontológicamente un estado de superposición? ¿Qué significa que un sistema cuántico se encuentre en un estado que es una superposición de autoestados de algún observable? Esta serie de preguntas no sólo retan nuestras intuiciones y convicciones ontológicas clásicas, sino que nos lleva a pensar en profundidad cuál es la naturaleza misma del estado cuántico y de los sistemas cuánticos. Cabe señalar que la superposición tiene manifestaciones empíricas como en el experimento de la doble rendija, donde el electrón se encuentra en un estado de superposición que da lugar a una interferencia observable.
Una primera forma de dar sentido a la noción de superposición de estados es considerar que, en realidad, no estamos tratando con estados superpuestos de un único sistema cuántico, sino que en realidad estamos lidiando con un estado global que refiere a una colección de sistemas idénticos, lo que a menudo se denomina “ensemble”. Defendida principalmente por Leslie Ballentine (1970) y Karl Popper (1982), bajo la influencia de Albert Einstein y su idea de la incompletitud de la mecánica cuántica (Einstein, Podolsky y Rosen 1935), esta interpretación estadística sostiene que una superposición es meramente el estado de un sistema formado por múltiples sistemas cuánticos que, en realidad, sí tienen estados y propiedades bien definidos (Hughes 1989). De acuerdo con Einstein:
“el intento de concebir la descripción teórico-cuántica como una descripción completa de los sistemas individuales conduce a interpretaciones tan poco naturales, que inmediatamente resultan ser innecesarias si uno acepta la interpretación que la descripción refiere a colecciones de sistemas y no a sistemas individuales” (Schilpp 1949, 671-2).
Naturalmente, todo halo misterioso y paradojal que rodea la existencia de superposiciones se desvanece ni bien se considera que la mecánica cuántica en realidad se refiere a colecciones de sistemas y no a sistemas individuales. Nada de desconcertante hay en que dentro de una colección haya una cierta cantidad de objetos con una propiedad y otra cierta cantidad de objetos con otra propiedad, y que podamos expresar el estado del conjunto mediante la combinación de los estados de los objetos que lo componen: hay en mi monedero 20 monedas plateadas y 25 monedas doradas, por lo tanto, el estado actual de mi billetera, considerando la cantidad total de monedas que tiene, puede expresarse como una superposición de estados de objetos de color plateado y de objetos de color dorado. De esta manera, es posible retener nuestros principios e intuiciones clásicas acerca de propiedades y objetos ya que, indubitablemente, cada moneda individual es o bien plateada o bien dorada.
Esta interpretación estadística o de ensembles resulta natural a la hora de dar sentido y comprender las implicancias físicas del principio de superposición. Sin embargo, esta interpretación encuentra dificultades en el propio marco teórico de la mecánica cuántica, en particular, cuando consideramos el teorema demostrado por Simon Kochen y Ernst Specker en 1967 (uno de los “no-go theorems” en mecánica cuántica, es decir, teoremas que demuestran que cierta situación física no es posible de acuerdo con la teoría). En esencia, el teorema demuestra que el supuesto según el cual todos los observables de un sistema cuántico poseen valores definidos en un mismo instante resulta insostenible, ya que conduce a una contradicción en el marco de la teoría. Este supuesto es una premisa de cualquier interpretación de la teoría que considere la existencia de propiedades definidas aunque inaccesibles empíricamente (variables ocultas), como la propia interpretación estadística (para una presentación detallada del teorema, ver Kochen y Specker 1967, Cabello, Estebaranz y García-Alcaine 1996, Carsten 2014; para una demostración técnica de cómo el teorema contradice la interpretación estadística, ver Hughes 1989, 164-168). En este sentido se habla de la contextualidad cuántica: en cada contexto parcial, definido por una base del espacio de Hilbert, quedan seleccionados los observables que adquieren valor definido en ese contexto, pero no es posible determinar los valores de todos los observables del sistema a la vez. Las dificultades que enfrenta la interpretación estadística frente al teorema de Kochen-Specker nos hace retroceder al punto de partida y enfrentarnos cara a cara, nuevamente, con la pregunta acerca de qué es una superposición. Ya no podemos pensar a la superposición como estados de conjuntos de sistemas, sino que tenemos que considerarlos estrictamente como estados de sistemas cuánticos individuales.
Existen varias interpretaciones que intentan no apelar a variables ocultas o a ensembles para hacer frente a este problema. El famoso físico alemán Werner Heisenberg (1959), uno de los padres fundadores de la mecánica cuántica, por ejemplo, sostuvo que “la función de probabilidad (…) contiene afirmaciones acerca de posibilidades o, mejor dicho, tendencias (‘potentia’ en la filosofía de Aristóteles)” (1959, 53). Según Heisenberg, por lo tanto, una superposición de estados no representa un estado actual del mundo, sino una posibilidad objetiva de un sistema cuántico de actualizar un cierto estado u otro. También apelando y poniendo el acento en la idea de posibilidad, aunque con un grado de desarrollo y sistematicidad mucho mayor y en un espíritu diferente al perseguido por Heisenberg, los seguidores de las interpretaciones modales de la mecánica cuántica (van Frassen 1972, 1974, 1991; Dieks 1989, 1994, 2010; Lombardi y Castagino 2008) conciben los estados dinámicos del sistema en términos de propiedades posibles, indicando cuáles son las probabilidades correspondientes (para una presentación de las diversas interpretaciones modales, ver Dieks y Vermaas 1998, Lombardi y Dieks 2016).
Mientras las interpretaciones modales dotan de realidad al dominio de lo posible, la interpretación de muchos-mundos expulsa la posibilidad del mundo cuántico. Sus principales defensores (Everett 1957, Deutsch 1999, 2002, Wallace 2012), argumentan que el vector de estado ![]() describe en realidad todo el universo, y todos los posibles estados de una superposición son o serán actuales en algunos de los mundos que pueblan el universo. La idea central es que, de acuerdo a la mecánica cuántica, el universo es una totalidad que constantemente se divide en infinitos mundos que actualizan los posibles estados de un sistema. Por ello no existe, estrictamente, posibilidad en el universo, ya que todo es actual al menos en un mundo. De acuerdo con esta interpretación, nosotros, como observadores pertenecientes a un mundo, sólo podemos acceder empíricamente a los valores que se han actualizado en ese mundo; sin embargo, los otros valores posibles se han actualizado en otros mundos tan reales como el nuestro, pero inaccesibles para nosotros. Por lo tanto, una superposición es un estado que describe el universo como un todo, con sus múltiples mundos en constante ramificación (para mayores detalles, ver Vaidman 2016, Allday 2009, Cap. 25; también puede consultarse la entrada Interpretaciones de la mecánica cuántica de esta misma enciclopedia).
describe en realidad todo el universo, y todos los posibles estados de una superposición son o serán actuales en algunos de los mundos que pueblan el universo. La idea central es que, de acuerdo a la mecánica cuántica, el universo es una totalidad que constantemente se divide en infinitos mundos que actualizan los posibles estados de un sistema. Por ello no existe, estrictamente, posibilidad en el universo, ya que todo es actual al menos en un mundo. De acuerdo con esta interpretación, nosotros, como observadores pertenecientes a un mundo, sólo podemos acceder empíricamente a los valores que se han actualizado en ese mundo; sin embargo, los otros valores posibles se han actualizado en otros mundos tan reales como el nuestro, pero inaccesibles para nosotros. Por lo tanto, una superposición es un estado que describe el universo como un todo, con sus múltiples mundos en constante ramificación (para mayores detalles, ver Vaidman 2016, Allday 2009, Cap. 25; también puede consultarse la entrada Interpretaciones de la mecánica cuántica de esta misma enciclopedia).
4 ¿Límite ontológico o mera ignorancia? Incerteza y contextualidad ↑
Mientras que, como señalamos en el apartado anterior, Paul Dirac afirmaba que el principio de superposición era la característica fundamental de la mecánica cuántica y uno de sus mayores desafíos, otros autores, como John von Neumann y Werner Heisenberg, consideraban que este lugar era ocupado por el principio de incerteza (también llamado principio de incertidumbre o de indeterminación, según cómo se interprete la naturaleza de esa incerteza. Discutiremos esto más adelante). Derivado del formalismo por Heisenberg en 1927, el principio de incerteza es no sólo una pieza central sino también un rasgo distintivo del formalismo de la mecánica cuántica. En términos generales, el principio afirma que existen pares de observables (es decir, propiedades de un sistema físico) a los cuales no es posible asignarles valores definidos de manera simultánea. Es decir, existiría en mecánica cuántica una limitación (¿ontológica?, ¿gnoseológica?) a la hora de determinar con precisión los valores de ciertas propiedades de un sistema físico al mismo tiempo. Naturalmente, este resultado trae consigo ciertas consecuencias a nivel ontológico que deben ser exploradas.
Para advertir en qué medida la mecánica cuántica y la física clásica divergen respecto del principio de incerteza, recurramos a nuestras intuiciones y convicciones ontológicas clásicas. Cuando pensamos en cualquier sistema físico clásico, no sólo consideramos que posee un número determinado de propiedades que lo describen, sino que, además, tenemos la convicción de que es posible determinar todas sus propiedades de manera simultánea para ofrecer una descripción completa del sistema. Es decir, todo objeto físico clásico está sujeto a lo que en metafísica comúnmente se conoce como principio de determinación omnímoda (omnimoda determatio), expuesto por Emmanuel Kant en la Crítica de la Razón Pura (2007 [1781/1787]): “toda cosa, por lo que respecta a su posibilidad, está además bajo el principio de determinación omnímoda, según el cual a ella le debe convenir uno de todos los posibles predicados de las cosas en la medida en que son comparados con sus contrarios” (A571, B600). El principio es intuitivamente claro y la física clásica parece respetarlo sin reservas. El libro que está sobre mi mesa instancia determinadas propiedades, como “ser pesado”, “ser de color negro”, “estar sobre mi mesa”, “tener cierto número de páginas”, etc. Una descripción detallada de todas sus propiedades nos daría una determinación completa del objeto, un conocimiento acabado de él. Naturalmente, yo podría cambiar su posición, arrancarle un cierto número de hojas o pintarlo de otro color; sin embargo, siempre tendrá una posición definida, un color determinado, un cierto número de hojas, etc., de manera simultánea. Obviamente, ciertos predicados no se pueden aplicar al objeto-libro, como “estar angustiado” o “estar sobre la mesa y estar sobre la biblioteca”: en el primer caso, adjudicarle ciertas propiedades al objeto puede constituir un error categorial, y en el segundo caso se viola el principio de no contradicción. De todas maneras, estas posibilidades quedan eliminadas por el propio principio de determinación omnímoda y no constituyen ningún problema para concebir las determinaciones de un objeto físico clásico.
El principio de incerteza desafía el alcance mismo del principio de determinación omnímoda: los objetos cuánticos tienen, de hecho, propiedades posibles que, sin embargo, no pueden estar determinadas simultáneamente. El principio afirma que existen observables que son incompatibles entre sí. Técnicamente, se considera que dos observables ![]() y
y ![]() son incompatibles cuando el conmutador entre sus operadores asociados es distinto de cero:
son incompatibles cuando el conmutador entre sus operadores asociados es distinto de cero: ![]() . Lo que Heisenberg descubrió fue que entre los observables cuánticos que no conmutan, se cumple una relación de incerteza. El ejemplo paradigmático de observables que no conmutan son la posición y el momento lineal; en este caso, la relación de incerteza se expresa:
. Lo que Heisenberg descubrió fue que entre los observables cuánticos que no conmutan, se cumple una relación de incerteza. El ejemplo paradigmático de observables que no conmutan son la posición y el momento lineal; en este caso, la relación de incerteza se expresa:
donde ![]() indica la desviación estándar de la posición y
indica la desviación estándar de la posición y ![]() la desviación estándar del momento lineal. Esto significa que, cuanto mayor sea la precisión en la determinación de la posición de un sistema cuántico (cuanto menor sea
la desviación estándar del momento lineal. Esto significa que, cuanto mayor sea la precisión en la determinación de la posición de un sistema cuántico (cuanto menor sea ![]() ), menor será la precisión en la determinación del momento (mayor será
), menor será la precisión en la determinación del momento (mayor será ![]() ), y viceversa, de modo tal que el producto entre las imprecisiones se mantenga dentro del rango fijado por
), y viceversa, de modo tal que el producto entre las imprecisiones se mantenga dentro del rango fijado por ![]() . La clave formal a partir de la cual se deriva el principio de incerteza radica en la posibilidad de expandir el estado de un sistema en diferentes bases, esto es, bases correspondientes a observables que no conmutan. Veamos este aspecto con más precisión.
. La clave formal a partir de la cual se deriva el principio de incerteza radica en la posibilidad de expandir el estado de un sistema en diferentes bases, esto es, bases correspondientes a observables que no conmutan. Veamos este aspecto con más precisión.
Supongamos un sistema cuántico con su propiedad ![]() , asociada al observable
, asociada al observable ![]() con autoestados
con autoestados ![]() , y su propiedad
, y su propiedad ![]() , asociada al observable
, asociada al observable ![]() con autoestados
con autoestados ![]() . No hay razón alguna para que los autoestados de
. No hay razón alguna para que los autoestados de ![]() y de
y de ![]() sean los mismos; en general, los autoestados de un operador se pueden expresar como combinación lineal de los autoestados del otro operador:
sean los mismos; en general, los autoestados de un operador se pueden expresar como combinación lineal de los autoestados del otro operador:
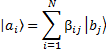
donde ![]() y
y ![]() para algún
para algún ![]() . Esto significa que las bases
. Esto significa que las bases ![]() y
y ![]() están “rotadas” una respecto de la otra; es decir, ambas bases del espacio de Hilbert no coinciden. En esta situación, si el sistema tiene la propiedad
están “rotadas” una respecto de la otra; es decir, ambas bases del espacio de Hilbert no coinciden. En esta situación, si el sistema tiene la propiedad ![]() definida en un valor
definida en un valor ![]() , entonces se encuentra en un estado definido: el autoestado
, entonces se encuentra en un estado definido: el autoestado ![]() de
de ![]() . Pero, según la sumatoria anterior, dicho estado se puede expresar como una superposición no trivial de los autoestados de
. Pero, según la sumatoria anterior, dicho estado se puede expresar como una superposición no trivial de los autoestados de ![]() . Esto significa que, en un caso genérico, si el sistema tiene definida la propiedad
. Esto significa que, en un caso genérico, si el sistema tiene definida la propiedad ![]() , entonces no tiene definida la propiedad
, entonces no tiene definida la propiedad ![]() . Es en este sentido que se dice que los observables
. Es en este sentido que se dice que los observables ![]() y
y ![]() son incompatibles: el sistema no puede tener ambas propiedades bien definidas a la vez, por razones que se siguen de manera estricta de la estructura formal de la teoría.
son incompatibles: el sistema no puede tener ambas propiedades bien definidas a la vez, por razones que se siguen de manera estricta de la estructura formal de la teoría.
Ahora bien, ¿cuáles son los problemas filosóficos que subyacen al principio de incerteza? Uno de los principales problemas radica en cuál es la naturaleza de esa incerteza, fundamentalmente, si ésta es de índole gnoseológica u ontológica: el principio, ¿expresa una limitación intrínseca de la teoría para describir los objetos cuánticos, al no ser capaz de brindar valores definidos de los observables? ¿O, por el contrario, la teoría describe un rasgo objetivo del mundo cuántico? Ya sea esta limitación de índole gnoseológica u ontológica, el principio de incerteza establece, al menos, un límite claro a los conceptos que clásicamente utilizamos para describir nuestro mundo cuando pretendemos utilizarlos en el dominio cuántico.
La interpretación estadística, que presentamos en la sección anterior, consideraría que el principio impone una mera limitación de nuestro conocimiento basado en la mecánica cuántica. A la manera de la mecánica estadística clásica en la versión gibbsiana, el vector de estado no representaría el estado de un único sistema cuántico sino la situación en la que se encuentra la colección o ensemble de sistemas similares. De esta manera, las probabilidades se convierten en frecuencias relativas dentro del ensemble y adquieren un significado exclusivamente gnoseológico: es una limitación de la teoría no poder definir con precisión los valores de cada sistema que componen el ensemble; pero, in re, los valores permanecen definidos: cada subsistema tiene todas sus propiedades determinadas de manera simultánea. Por lo tanto, es nuestra ignorancia acerca de tales valores y el recurso a frecuencias relativas lo que nos conduciría al principio de incerteza. Cualquier interpretación que considere que la mecánica cuántica no es una teoría completa y que existen “variables ocultas”, dotará al principio de incerteza de un contenido meramente gnoseológico: el hecho de que no se pueda asignar valores simultáneos de manera precisa a dos observables incompatibles no es un límite de la naturaleza, un límite in re. Un acérrimo defensor de este punto de vista fue Albert Einstein quien apeló a diferentes tipos de experimentos mentales (como el del reloj en la caja o el popular experimento EPR, al cual nos referiremos más adelante) para refutar la idea de que el principio de incerteza expresa un tipo de indeterminación ontológica o que constituye una ley fundamental de la naturaleza.
Sin embargo, apelando nuevamente al teorema de Kochen-Specker y a la contextualidad cuántica, en general se considera que el principio de incerteza sí representa una característica objetiva del mundo. La probabilidad cuántica no puede concebirse como medida de la ignorancia acerca de un micro-estado clásico subyacente en el cual se encontraría el sistema, sino que mide una indeterminación objetiva. No es la mecánica cuántica la que nos ofrece una descripción parcial del micromundo: es el propio micromundo el que posee características totalmente ajenas a las del mundo clásico. Es a la luz de esta idea que surgen genuinos problemas ontológicos: ¿el principio de incerteza contradice el principio de determinación omnímoda? Más aún, ¿qué clase de objeto es aquél cuyas propiedades no pueden determinarse de manera completa y simultánea?
A modo de ilustración, supongamos un objeto que tiene las propiedades de “pesar cierta cantidad de kilos” y “tener una altura”. Este objeto, además, se comporta según las leyes de la mecánica cuántica y, por lo tanto, cae bajo el alcance del principio de incerteza y de la contextualidad. Supongamos que “peso” y “altura” constituyen un par de observables incompatibles. Como primera acción para describir nuestro objeto, preparamos nuestro aparato de medición para determinar cuál es su peso. Luego de pesar el objeto, obtenemos un valor preciso: 13.5kg. Sin embargo, por haber llevado a cabo una medición muy precisa sobre una de sus propiedades, hemos perdido total información acerca de cuál es su altura (como explicamos técnicamente más arriba). Mientras conocemos su peso, desconocemos absolutamente su altura, siempre y cuando pretendamos conocer ambas propiedades a la vez. Esto es, sin lugar a dudas, algo extraño pero una consecuencia incuestionable del formalismo de la mecánica cuántica.
Sin embargo, este no es el final de la historia y los alcances del principio pueden ser llevados un paso más allá. Aceptado el principio de incerteza, sabemos que no podemos medir simultáneamente ambos observables con precisión, sino que, o bien medimos uno u otro con precisión, o bien nos conformamos con obtener un rango de valores de ambos observables, como por ejemplo: “mi objeto pesa entre 10-15kg., y tiene una altura de entre 40-50cm”. Pero, obstinados en nuestras convicciones clásicas, podríamos idear una manera de burlar el principio de incerteza y obtener una descripción completa aunque no simultánea. Para empezar, podríamos pesar el objeto, obteniendo un valor preciso de su peso y luego medir la altura del objeto, y así obtener un valor preciso de su altura. Si bien simultáneamente no es posible precisar ambas propiedades, parece plausible poder hacerlo procediendo en instantes distintos. Finalmente, parece que hemos obtenido la información completa que describe al objeto: “mi objeto pesa 13.5kg y mide 46cm”, burlando el principio de incerteza, aun así sea de manera no simultánea.
No obstante, hemos sido víctimas de nuestra ingenuidad clásica y de no comprender acabadamente el alcance de la contextualidad cuántica. Al considerar que el objeto pesa 13.5kg y mide 46cm, suponemos que el valor del peso se mantiene definido cuando efectuamos la medición de la altura y también obtenemos un valor definido. Pero esto es justamente lo que no permite el teorema de Kochen-Specker, que demuestra que cualquier asignación de valores precisos a todos los observables de un sistema cuántico conduce a una contradicción. En nuestro ejemplo, si el objeto pesa 13.5kg, asumir que tiene un valor preciso x de altura resulta contradictorio en el marco de la teoría, independientemente de cuál sea el valor x. Esto significa que, si el principio de incerteza dejaba aún abierta la posibilidad de una lectura gnoseológica de tal incerteza (x tiene un valor definido pero no sabemos cuál), la contextualidad cuántica frustra dicha interpretación: si el objeto tiene un valor definido de peso, no puede tener valor definido de altura, independientemente de si conocemos o no dicho valor, ya que, de suponerlo así, el formalismo cuántico nos conducirá a tener que admitir la verdad de un enunciado del tipo “p y no p”.
¿Cómo concebir estos peculiares objetos que parecen violar el principio de determinación omnímoda? Este es uno de los problemas ontológicos centrales de la mecánica cuántica, que no encuentran solución en ninguna interpretación no contextual, sea por ensembles o, en general, por variables ocultas. Lamentablemente, Einstein ya no estaba aquí cuando se formuló el teorema de Kochen-Specker: habría sido por demás interesante conocer su postura frente a tan importante resultado teórico.
5 ¿Hay realidad más allá de medir? El problema de la medición ↑
En los apartados anteriores encontramos problemas ontológicos vinculados con la existencia de estados superpuestos y de observables incompatibles entre sí. En ambos casos, nos referimos repetidamente al acto de medir algún observable relevante del sistema: en primer lugar notamos que, a pesar de la existencia de la superposición, de acuerdo al formalismo de la mecánica cuántica siempre medimos valores definidos; luego subrayamos la existencia de un límite para nuestras mediciones, establecido por el principio de incerteza. Estrechamente vinculado a estos problemas, el proceso de medir mismo también involucra una serie de complejidades y problemas que no tienen análogo clásico. Jeffrey Bub (1997) ha afirmado que el llamado “problema de la medición” constituye un problema central y de vital importancia en mecánica cuántica. Aquí pondremos el foco en las consecuencias del problema en el plano ontológico, considerando qué es una medición, y en particular, una medición de un sistema cuántico.
De manera general, el proceso de medir alguna propiedad de un sistema físico con un dispositivo determinado implica algún grado de interacción y correlaciones entre ambos sistemas. Cuando queremos medir la intensidad de una corriente eléctrica, sabemos que la corriente interactúa con el circuito interno del amperímetro, donde observamos directamente los valores medidos: confiamos en que esos valores guardan algún tipo de relación con la propiedad medida del sistema: “el resultado de la medición es el estado del aparato de medición luego de que ha interactuado con el sistema, un estado que podemos ratificar observando directamente el dispositivo” (Lange 2002, 256). Por supuesto, toda medición científica involucra márgenes de error ya que no existen aparatos absolutamente precisos (para un abordaje completo sobre mediciones en ciencia, ver Alder 2002 o Tal 2015). Sin embargo, de manera ideal, puede definirse el acto de medir como un proceso en el cual el resultado de la medición está perfectamente correlacionado con el estado de un sistema con el cual ha interactuado (Lange 2002, van Frassen 2008, Tal 2015).
Para el caso concreto de las mediciones cuánticas, John von Neumann (1932) formuló el siguiente modelo de medición. Consideremos un sistema ![]() , con una propiedad
, con una propiedad ![]() asociada al observable
asociada al observable ![]() y un aparato de medición
y un aparato de medición ![]() diseñado para medir la propiedad
diseñado para medir la propiedad ![]() . El proceso de medición consta de tres etapas:
. El proceso de medición consta de tres etapas:
1. Condición inicial. En un primer momento, el sistema ![]() a medir y el aparato de medición
a medir y el aparato de medición ![]() no interactúan: cada uno se encuentra en su estado inicial independiente. Inicialmente
no interactúan: cada uno se encuentra en su estado inicial independiente. Inicialmente ![]() se encuentra en una superposición de los autoestados
se encuentra en una superposición de los autoestados ![]() del observable
del observable ![]() :
:
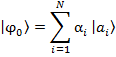
Al inicio, el aparato ![]() se encuentra listo para medir, en el estado
se encuentra listo para medir, en el estado ![]() , autoestado del observable
, autoestado del observable ![]() que actúa como puntero. Entonces, el estado inicial del conjunto es:
que actúa como puntero. Entonces, el estado inicial del conjunto es:
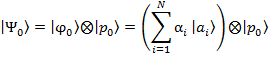
Donde ![]() es el estado del sistema compuesto
es el estado del sistema compuesto ![]() antes de que se produzca la interacción.
antes de que se produzca la interacción.
2. Interacción. En una segunda etapa, ![]() y
y ![]() entran en interacción y se producen las correlaciones. Cada autoestado
entran en interacción y se producen las correlaciones. Cada autoestado ![]() del observable
del observable ![]() del sistema
del sistema ![]() se correlaciona con un autoestado
se correlaciona con un autoestado ![]() del puntero
del puntero ![]() del aparato de medición
del aparato de medición ![]() :
:
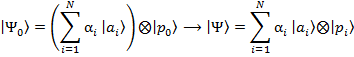
Esto significa que a cada estado posible ![]() del sistema le corresponde una indicación
del sistema le corresponde una indicación ![]() del puntero del aparato. La correlación entre los posibles estados del sistema y las posibles indicaciones del puntero nos permiten decir que se está midiendo el sistema
del puntero del aparato. La correlación entre los posibles estados del sistema y las posibles indicaciones del puntero nos permiten decir que se está midiendo el sistema ![]() , en particular, su propiedad
, en particular, su propiedad ![]() .
.
3. Lectura. En la última etapa los sistemas dejan de interactuar y es posible efectuar la lectura del puntero. Como en la práctica el puntero (por ejemplo, una aguja en un dial) no se encuentra en una superposición, se espera que de algún modo uno de los valores posibles del puntero resulte seleccionado:
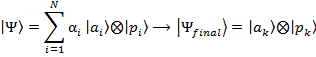
De esta manera podría afirmarse que el puntero indica el valor ![]() .
.
Intuitivamente, el proceso de medir nos estaría brindando información acerca de cuál era el estado del sistema previo a ser medido: el aparato de medición meramente nos indica dicho estado determinado. Sin embargo, nada es tan sencillo en mecánica cuántica, y por ello el problema de la medición ha agitado tantas aguas y causado arduas discusiones en la bibliografía científica y filosófica. Pero ¿en qué consiste, precisamente, el problema de la medición?
En el apartado dedicado al problema de la superposición, mencionamos rápidamente las líneas generales del problema: cómo explicar que los aparatos de medición arrojen valores definidos para las propiedades de los sistemas cuánticos cuando tales sistemas se encuentran en una superposición de estados. En referencia al modelo de von Neumann para una medición cuántica, el problema radica en encontrar un proceso físico que permita reproducir lo que se espera hallar en la etapa de lectura. En palabras de Niels Bohr, el núcleo del problema radica en el proceso mismo de medir: “el procedimiento de medición tiene una influencia esencial sobre las condiciones en las cuales la propia definición de propiedad física descansa” (Bohr 1935, 1025). Otra manera de enfocar la situación es en términos de un conflicto entre la dinámica lineal del sistema cuántico antes de ser medido y la aparente necesidad de una evolución no lineal que explique lo obtenido luego de la medición (Krips 2016).
La respuesta canónica (y la más difundida) a este problema consistió en apelar a un postulado externo a la teoría, es decir, que no se sigue del formalismo y los principios de la mecánica cuántica: el “postulado del colapso” o la “reducción de la función de onda”. Originalmente propuesto por Heisenberg en 1927, fue adoptado por la llamada interpretación de Copenhague (para mayor información acerca de esta interpretación, ver Hooner 1987, Allday 2009, cap.24, Faye 2014) y se convirtió en la explicación ortodoxa del problema en el ámbito de la comunidad científica. Desde esta perspectiva, el estado de un sistema cuántico puede seguir dos tipos de evoluciones: cuando no es medido, evoluciona según la ecuación de Schrödinger, de manera determinista, unitaria, lineal y reversible (Pessoa 2005, 45); pero, cuando se realiza una medición sobre el sistema, el estado “colapsa”, interrumpiendo la evolución unitaria según la ecuación de Schrödinger. Si antes de efectuar la medición el sistema cuántico se encontraba en un estado de superposición respecto de un observable, cuando se lleva a cabo la medición el estado colapsa en alguno de los autoestados de tal observable, ofreciendo los valores clásicos que obtenemos en el aparato de medición a través de una evolución no unitaria e indeterminista. Por ejemplo, si existe una distribución de probabilidades sobre la posición de una partícula, cuando se lleva a cabo la medición la posición se define completamente en un punto determinado del espacio.
A pesar de ser sumamente efectivo, el postulado del colapso no está exento de problemas interpretativos y, si bien muy popular y difundido entre la comunidad de físicos, ha recibido numerosas críticas. En principio, la existencia de dos tipos muy distintos de evoluciones parece, al menos, extraña. David Albert señala al respecto:
“La dinámica [de la teoría] y el postulado del colapso están categóricamente en contradicción (…) el postulado del colapso parece estar en lo cierto acerca de qué sucede cuando medimos, y la dinámica parece estar bizarramente equivocada acerca de qué sucede cuando medimos, y todavía, la dinámica parece estar en lo cierto acerca de qué sucede siempre que no estamos midiendo” (Albert 1992, 79).
Usualmente, la hipótesis del colapso es cuestionada porque se fundamenta en una noción de “medición” que no ha sido analizada cuidadosamente pero que, sin embargo, juega un papel físico fundamental a la hora de establecer las propiedades de una evolución cuántica (Dickson 2007, 363): ¿qué tiene de físicamente especial el proceso de medir? Desde una perspectiva más general, físicamente, ¿qué es una medición? Si la mecánica cuántica es una teoría fundamental, debería decirnos qué es una medición; sin embargo, la hipótesis del colapso, estrechamente relacionada con el proceso de medir, introduce una fuerte dependencia contraria: es la medición la que nos dice qué es la mecánica cuántica. (Dickson 2007). Por otro lado, al asumirse de manera acrítica la idea de medición, no hay claridad acerca de qué distingue una medición de otras interacciones físicas. La hipótesis del colapso puede también considerarse conceptualmente inadecuada por describir un proceso introducido ad hoc a la hora de explicar el fenómeno de medir, ya que (ver Lombardi, Fortin, Castagnino y Ardenghi 2011):
- No se ofrece una explicación de las causas que producen el colapso, ni se indica el instante en el que éste se produce.
- El postulado por sí solo no explica por qué el sistema colapsa en una determinada base y no en otra.
- Puesto que el colapso se produce en el sistema total, se trata de un fenómeno no-local, en el sentido de que no tiene en cuenta la distancia a la que se encuentran el sistema y el aparato.
Algunas interpretaciones de la mecánica cuántica han intentado mitigar las dificultades de la hipótesis del colapso considerando que el colapso se produce de manera espontánea –rompiendo el vínculo colapso y proceso de medición– cada cierta cantidad de tiempo (Ghirardi, Rimini y Weber 1986. Para una exposición general puede consultarse Ghirardi 2016). Por su parte, Heisenberg consideraba que el estado cuántico era una descripción objetiva de la potencialidad del objeto (es decir, de sus propiedades posibles). El sistema cuántico adquiere propiedades actuales y definidas solamente después de ser medido. Desde este punto de vista, el colapso no es sino el paso de la potencia a la actualidad, el paso a la existencia de las propiedades de un sistema cuántico (Heisenberg 1959). Mientras tanto, de acuerdo con Bohr, el problema de la medición simplemente mostraba que una “realidad independiente en el sentido ordinario no puede adscribirse a los fenómenos ni a la acción de medir” (Bohr 1935, 1025). Según el autor, lo que el problema de la medición pone en evidencia es que el estado de un sistema cuántico no tiene existencia independiente del aparato de medición y sólo adquiere pleno sentido físico cuando es considerado como el estado combinado del sistema a medir y el aparato de medición. Esta incapacidad de escindir ambos sistemas permite a Bohr salvaguardar cierto rasgo de clasicidad: el sistema cuántico siempre tendrá propiedades clásicas y definidas en el contexto de una medición (Allday 2009, 417).
Naturalmente, otras interpretaciones de la mecánica cuántica han buscado hacer frente al problema de la medición prescindiendo de la hipótesis del colapso. Por ejemplo, las interpretaciones modales proponen eliminar tal postulado de la teoría ya que consideran la medición cuántica como una interacción física ordinaria. No hay colapso en la dinámica del estado: éste siempre evoluciona unitariamente de acuerdo a la ecuación de Schrödinger. No obstante, las interpretaciones modales distinguen el plano de lo posible del plano de lo actual a través de la distinción entre “estados dinámicos” y “estados-valor”. El estado dinámico del sistema, representado por un vector de estado, describe lo posible, es decir, brinda las probabilidades para los distintos valores posibles de todos los observables del sistema. El estado dinámico nunca colapsa: las probabilidades evolucionan siempre lineal y unitariamente según la ecuación de Schrödinger. Sin embargo, el sistema cuántico tiene también ciertas propiedades actuales bien definidas, es decir, valores definidos de algunas magnitudes físicas (obviamente, no de todas, dada la restricción que impone el teorema de Kochen y Specker).
El problema de la medición recoge y agudiza algunos de los problemas ontológicos mencionados en las secciones anteriores. A su vez, las respuestas que cada interpretación ofrece al problema dan lugar a nuevas y variadas inquietudes ontológicas. Por ejemplo, en el marco de las interpretaciones modales, las probabilidades que el estado cuántico asigna a los valores posibles de los observables de un sistema suelen ser interpretadas de manera objetiva (Kochen 1985, Dieks 1989, Bene y Dieks 2002, Lombardi y Castagnino 2008), mientras que la interpretación de muchos mundos considera que la probabilidad es meramente gnoseológica, ya que cada valor posible encuentra su actualización en algún mundo, o bien el nuestro, o bien otro separado e inaccesible para nosotros (Everett 1957, Greaves 2006, Vaidman 2016, Wallace 2012). Por lo tanto, qué tipo de respuesta se brinde al problema de la medición y qué interpretación se adopte para ello, nos compromete con una cierta naturaleza de las probabilidades cuánticas, y ello se relaciona de manera estrecha con cuál es la ontología de la mecánica cuántica.
Por otro lado, las dificultades que involucra el proceso de medición cuántica plantean un genuino problema acerca de qué tipo de realidad cuántica existe independientemente del aparato de medición. Haciéndonos eco de las palabras de Bohr y Heisenberg, ¿en qué medida podemos atribuir realidad independiente al sistema medido si, cuando queremos obtener algún tipo de información acerca de sus propiedades, inevitablemente resulta entrelazado con el aparato de medir? ¿Es que sólo tiene sentido atribuir realidad al sistema compuesto de “aparato de medir” más “sistema medido”? Como mencionamos anteriormente, en el marco de la interpretación de Copenhague no puede adjudicarse ningún tipo de realidad independiente al sistema cuántico. En palabras de Heisenberg: “lo que observamos no es la naturaleza misma, sino la naturaleza expuesta a nuestro modo de indagarla” (1956). Desde esta perspectiva, la potentia que los estados cuánticos poseen entre mediciones posee un grado de realidad disminuido y claramente ambiguo. Por el contrario, las interpretaciones modales han afirmado el carácter real e irreductible de la posibilidad. Por ejemplo, la interpretación modal-Hamiltoniana (Lombardi y Castagnino 2008) afirma que la mecánica cuántica describe el reino de lo posible, reino irreductible a lo actual donde los hechos posibles tienen tanta realidad como los hechos actuales. Por lo tanto, para esta interpretación, entre una medición y otra existe una realidad posible con estatus ontológico propio y la mecánica cuántica describe esa realidad.
6 ¿Hay objetos cuánticos? El problema de la individualidad de las partículas ↑
Hasta el momento nos hemos referido a problemas ontológicos que involucran a un solo sistema cuántico. Más aún, siempre nos hemos referido a los sistemas cuánticos como si fuesen objetos con una cierta unidad e individualidad; también nos hemos referido a ellos como teniendo tal o cual estado, portando o instanciando ciertas propiedades. En síntesis, nos hemos referido a ellos como si, “por debajo” de las propiedades (observables), hubiese una suerte de objeto físico, en el sentido de una sustancia concreta, singular e individualizable. Sin embargo, la misma noción de “objeto individual” para referirnos a los sistemas cuánticos puede ser puesta en duda a la luz de ciertos fenómenos y resultados de la teoría.
Filosóficamente, la noción de “objeto” es difícil de aprehender de manera acabada: el concepto resulta tan amplio que es difícil brindar una definición precisa que abarque todas las características mediante las cuales identificamos objetos. En términos generales, pueden encontrarse dos tipos de enfoques frente a la pregunta acerca de qué es un objeto: un enfoque semántico y un enfoque metafísico (Lowe 1995). De acuerdo con el primero, un objeto es aquello a lo cual nos referimos mediante términos singulares (Frege 1977 [1892], Dummet 1973) o aquello que puede ser el valor de una variable cuantificada (Quine 1953). En cambio, de acuerdo al enfoque metafísico, un objeto es una entidad que posee determinadas condiciones de identidad (Lowe 1995, Wetzel 2008). Esta discusión suele relacionarse de manera muy estrecha con otra noción, la de individuo: qué es un individuo, qué es aquello que permite individualizar objetos. La naturaleza de los individuos ha sido sumamente discutida en la bibliografía filosófica, constituyendo una de las principales controversias metafísicas. Tradicionalmente, un objeto individual es algo que puede ser identificado en el espacio y en el tiempo (es decir, que tiene una localización espacial y temporal precisa), posee cierta independencia, es diferente de otro individuo y tiene una unidad intrínseca. Suele decirse que un individuo posee algún tipo de principio de individualidad que lo hace distinto de otros individuos pero lo hace ser el mismo a través del tiempo.
La idea de que un individuo es una sustancia (que opera como principio de individualidad) más propiedades (que son contingentes y pueden cambiar) es una de las concepciones más difundidas en la metafísica tradicional, asumiendo diferentes formas. La idea puede rastrearse, si bien con un sentido diferente, hasta Aristóteles (Categorias, Metafísica), y adquiere su forma más explícita en la doctrina de la sustancia de John Locke (1999 [1690]) o las mónadas en la filosofía de Gottfried Leibniz (1983 [1686]). Desde un punto de vista lógico y lingüístico, un individuo puede ser nombrado o caer bajo descripciones definidas. Los sistemas de lógica usuales también presuponen alguna noción de individuo en la medida en que variables y constantes son sujetos de predicación: el rango de variables constituye el dominio de los individuos a los cuales las propiedades se aplican (para una discusión pormenorizada de la noción metafísica de individuo y sustancia, ver Robinson 2014).
¿Qué puede decirse acerca de la noción de objeto o individuo en mecánica cuántica? ¿Son los sistemas cuánticos (v.g. partículas como electrones, fotones, etc.), más allá de algunas características y comportamientos peculiares, objetos, en algún sentido, como lo son los sistemas clásicos? En este apartado expondremos y analizaremos las respuestas a estas preguntas a partir de dos fenómenos cuánticos muy conocidos: la no-separabilidad y la indistinguibilidad de las partículas cuánticas. La bibliografía en torno a estos fenómenos es muy amplia y ha dado lugar a grandes discusiones en la comunidad de físicos y filósofos. Aquí nos limitaremos a analizar cómo estos fenómenos ponen en discusión la idea de que los sistemas cuánticos puedan considerarse objetos en sentido estricto. El fenómeno de la no-separabilidad cuestiona tanto la noción de objeto cuántico individual como el principio metafísico de reducción y composicionalidad: cuando dos sistemas cuánticos interactúan y forman un sistema compuesto, no sólo ya no es posible re-identificar las partes componentes, sino que el sistema compuesto se comporta de manera holista y no-local. Por su parte, el carácter indistinguible de las partículas cuánticas conduce a cuestionarnos los criterios de identidad de los sistemas cuánticos, despertando toda una serie de preguntas metafísicas, como por ejemplo: si dos partículas cuánticas son indistinguibles, ¿qué motivos tenemos para sostener que hay dos partículas?
6.1 No-separabilidad ↑
Comencemos explicando a qué nos referimos cuando afirmamos que dos sistemas físicos son separables. De acuerdo con la mecánica newtoniana clásica, si dos objetos interactúan y luego se separan, no es posible afectar los estados de uno de ellos mediante una acción local sobre el otro. En función de esta razonable suposición, se puede formular el siguiente principio de separabilidad:
“Los contenidos de dos regiones espacio-temporales cualesquiera separadas por un intervalo espacio-temporal que no se anula constituyen sistemas físicos separables, en el sentido que (1) cada uno posee su propio y distinto estado físico, y (2) el estado compuesto de los dos sistemas está totalmente determinado por los estados de los sistemas separados” (Howard 1989, 225-6).
El punto neurálgico de la no-separabilidad cuántica radica en que, cuando dos sistemas cuánticos interactúan, sus estados quedan entrelazados de tal manera que violan este principio de separabilidad: no sólo sus estados ya no pueden considerarse independientes y propios de cada sistema, sino que el estado compuesto por ambos sistemas no queda determinado por la mera combinación de los estados de los subsistemas. Este último fenómeno viola otro principio usual de la metafísica tradicional: el principio de reducción y de composicionalidad, según el cual “un todo, tal como un par de partículas, no es más que la suma de sus partes –es decir, el todo se reduce a sus partes” (Lange 2002, 289). Esta no-separabilidad en mecánica cuántica posee una clara expresión en el formalismo de la teoría.
Consideremos un par de sistemas cuánticos: el sistema ![]() se encuentra en el estado
se encuentra en el estado ![]() - y el sistema
- y el sistema ![]() en el estado
en el estado ![]() ; ambos sistemas están separados, son independientes uno del otro y nunca antes han interactuado. Como fue señalado en la Sección 1, antes de la interacción, los dos sistemas pueden considerarse subsistemas de un sistema compuesto
; ambos sistemas están separados, son independientes uno del otro y nunca antes han interactuado. Como fue señalado en la Sección 1, antes de la interacción, los dos sistemas pueden considerarse subsistemas de un sistema compuesto ![]() cuyo estado inicial es el producto tensorial de los estados de ambos subsistemas:
cuyo estado inicial es el producto tensorial de los estados de ambos subsistemas:
Ahora bien, supongamos que ambos sistemas interactúan físicamente durante un tiempo finito. Una interacción posible es la que convierte el estado total del sistema compuesto en lo que se denomina “estado singlete”, que correlaciona perfectamente los estados posibles de los sistemas componentes. Se dice que los estados de los dos sistemas quedan entrelazados (“entangled”):
La correlación indica que (i) si el sistema ![]() se encuentra en el estado
se encuentra en el estado ![]() , entonces el sistema
, entonces el sistema ![]() se encuentra en el estado
se encuentra en el estado ![]() (primer término de la expresión de
(primer término de la expresión de ![]() ), y (ii) si el sistema
), y (ii) si el sistema ![]() se encuentra en el estado
se encuentra en el estado ![]() , entonces el sistema
, entonces el sistema ![]() se encuentra en el estado
se encuentra en el estado ![]() (segundo término de la expresión de
(segundo término de la expresión de ![]() ). La característica peculiar de los estados singlete es que no pueden formarse como producto tensorial de estados que correspondan a
). La característica peculiar de los estados singlete es que no pueden formarse como producto tensorial de estados que correspondan a ![]() y
y ![]() de manera separada e independiente, como sucedía antes de la interacción. Es importante resaltar que esta característica no sólo se da mientras los sistemas se encuentran en interacción, sino que permanece indefinidamente luego de la interacción: el entrelazamiento no desaparece cuando la interacción ha finalizado y no disminuye con la distancia ni con el tiempo durante la ulterior evolución.
de manera separada e independiente, como sucedía antes de la interacción. Es importante resaltar que esta característica no sólo se da mientras los sistemas se encuentran en interacción, sino que permanece indefinidamente luego de la interacción: el entrelazamiento no desaparece cuando la interacción ha finalizado y no disminuye con la distancia ni con el tiempo durante la ulterior evolución.
Sobre esta base, puede explicarse en qué sentido se habla de no-separabilidad en mecánica cuántica. En primer lugar, debe señalarse que el sistema compuesto ![]() posee observables (propiedades posibles) que no pertenecen a ninguno de los dos subsistemas componentes ni se obtienen como suma de observables de tales subsistemas. Por ejemplo, si consideramos el observable
posee observables (propiedades posibles) que no pertenecen a ninguno de los dos subsistemas componentes ni se obtienen como suma de observables de tales subsistemas. Por ejemplo, si consideramos el observable ![]() representado por el operador
representado por el operador ![]() en el sistema
en el sistema ![]() y el observable
y el observable ![]() representado por el operador
representado por el operador ![]() en el sistema
en el sistema ![]() , el operador
, el operador ![]() representa una propiedad del sistema compuesto que no puede obtenerse como resultado de una operación algebraica entre los operadores que representan los observables
representa una propiedad del sistema compuesto que no puede obtenerse como resultado de una operación algebraica entre los operadores que representan los observables ![]() y
y ![]() . En palabras sencillas, el sistema compuesto posee más propiedades que los sistemas componentes, y muchas de ellas no pueden reducirse a las propiedades de los sistemas componentes. En este sentido, la mecánica cuántica viola el principio metafísico de reducción y de composicionalidad: el todo es más que la “suma” de sus partes.
. En palabras sencillas, el sistema compuesto posee más propiedades que los sistemas componentes, y muchas de ellas no pueden reducirse a las propiedades de los sistemas componentes. En este sentido, la mecánica cuántica viola el principio metafísico de reducción y de composicionalidad: el todo es más que la “suma” de sus partes.
Puesto que el entrelazamiento no desaparece luego de que la interacción ha finalizado y no disminuye durante la ulterior evolución, es posible tomar cada uno de los sistemas ![]() y
y ![]() y llevarlos a laboratorios distintos sin alterar el estado total. Una vez separados espacialmente, no importa cuál sea la distancia, no es posible seguir considerándolos sistemas independientes: la correlación establecida entre ambos se mantiene a pesar de la distancia y a través del tiempo. Por lo tanto, los resultados de las posibles mediciones que se efectúen sobre
y llevarlos a laboratorios distintos sin alterar el estado total. Una vez separados espacialmente, no importa cuál sea la distancia, no es posible seguir considerándolos sistemas independientes: la correlación establecida entre ambos se mantiene a pesar de la distancia y a través del tiempo. Por lo tanto, los resultados de las posibles mediciones que se efectúen sobre ![]() y
y ![]() también estarán correlacionados. Supongamos que el estado
también estarán correlacionados. Supongamos que el estado ![]() es autoestado de un observable
es autoestado de un observable ![]() con autovalor
con autovalor ![]() , y el estado
, y el estado ![]() es autoestado de un observable
es autoestado de un observable ![]() con autovalor
con autovalor ![]() . Cuando el sistema compuesto se encuentra en el estado singlete
. Cuando el sistema compuesto se encuentra en el estado singlete ![]() , (i) si una medición del observable
, (i) si una medición del observable ![]() sobre el subsistema
sobre el subsistema ![]() da como resultado el valor
da como resultado el valor ![]() , la medición del observable
, la medición del observable ![]() sobre el subsistema
sobre el subsistema ![]() dará como resultado el valor
dará como resultado el valor ![]() ,con certeza (ver primer término de la expresión de
,con certeza (ver primer término de la expresión de ![]() ), y (ii) si una medición del observable
), y (ii) si una medición del observable ![]() sobre el subsistema
sobre el subsistema ![]() da como resultado el valor
da como resultado el valor ![]() , la medición del observable
, la medición del observable ![]() sobre el subsistema
sobre el subsistema ![]() dará como resultado el valor
dará como resultado el valor ![]() con certeza (ver segundo término de la expresión de
con certeza (ver segundo término de la expresión de ![]() ). En otras palabras, una medición sobre
). En otras palabras, una medición sobre ![]() cambia la distribución de probabilidades sobre un observable de
cambia la distribución de probabilidades sobre un observable de ![]() , aunque no hayamos llevado a cabo ninguna acción local sobre
, aunque no hayamos llevado a cabo ninguna acción local sobre ![]() . En este sentido preciso se dice que los sistemas son no-separables y que la mecánica cuántica viola el principio de separabilidad tal como fue anteriormente enunciado.
. En este sentido preciso se dice que los sistemas son no-separables y que la mecánica cuántica viola el principio de separabilidad tal como fue anteriormente enunciado.
A su vez, si estos experimentos se conciben desde el punto de vista de la hipótesis del colapso, aparecen nuevas consecuencias: la no-separabilidad implica que cualquier medición que haga colapsar el sistema ![]() produce el colapso (un cambio instantáneo) del estado del sistema
produce el colapso (un cambio instantáneo) del estado del sistema ![]() . Lo particularmente sorprendente de esta situación es que los sistemas
. Lo particularmente sorprendente de esta situación es que los sistemas ![]() y
y ![]() ya no se encuentran en interacción (al menos de manera local) y están espacialmente separados por una distancia arbitrariamente grande; sin embargo, aun así es posible producir modificaciones del estado de uno de los sistemas mediante acciones locales sobre el otro. De este modo, a la luz de la hipótesis del colapso la no-separabilidad conduce a una forma de no-localidad.
ya no se encuentran en interacción (al menos de manera local) y están espacialmente separados por una distancia arbitrariamente grande; sin embargo, aun así es posible producir modificaciones del estado de uno de los sistemas mediante acciones locales sobre el otro. De este modo, a la luz de la hipótesis del colapso la no-separabilidad conduce a una forma de no-localidad.
Esta clase de situaciones ha dado lugar al llamado “problema de la no-separabilidad” o “problema de la no-localidad”, que ha sido sumamente discutido en la bibliografía científica y filosófica sobre mecánica cuántica. Probablemente uno de los más famosos experimentos mentales en física sea la famosa “paradoja” de Einsten, Boris Podolsky y Nathan Rosen (1935) o, como usualmente se lo conoce, el “experimento EPR”. Si bien el objetivo fundamental de los autores fue mostrar que la mecánica cuántica era una teoría incompleta y que, por lo tanto, no ofrecía una descripción adecuada de la realidad física, el planteo del experimento y la posterior discusión que se generó a su alrededor viró hacia el problema de la no-separabilidad (Bohr 1935, 1959, Bohm y Aharanov 1957, Born 1971; para una exposición actual de los problemas relativos al experimento de EPR, ver Fine 2014). Si bien concebido originalmente por Einstein, Podolsky y Rosen como un experimento mental, experimentos tipo EPR han sido realizados en el laboratorio a partir de la década del ‘80 (ver Aspect, Grangier y Roger 1982, Hensen et al. 2015).
En particular, vale la pena distinguir dos tipos de discusión: por un lado, acerca de si la mecánica cuántica aboga o no por una ontología holista; por otro lado, acerca de si la mecánica cuántica implica o no una realidad no-local. Respecto del primer caso, una ontología holista sostiene que la naturaleza de una totalidad no está determinada por la naturaleza de sus partes (ejemplo paradigmático es el caso de la mecánica cuántica Bohmiana, ver Bohm 1952) o, en términos de propiedades, los objetos tienen propiedades que no están determinadas por las propiedades físicas de sus constituyentes (para más detalles acerca del debate sobre diferentes tipos de holismo y sobre el holismo en mecánica cuántica, ver Teller 1986, Maudlin 1998, Esfeld 2001, Healey 2016). Respecto del segundo caso, una realidad no-local implica la existencia de algún tipo de acción a distancia, esto es, la existencia de causas que podrían actuar de manera no-local. Para algunos autores, la posibilidad de una realidad no-local no es sugerida sólo por experimentos como EPR, sino también por los teoremas de Bell (para más detalles y discusión al respecto, ver Bell 1964, Maudlin 1994, Lange 2002, Berkovitz 2016).
6.2 Indistinguibilidad ↑
Hasta el momento hemos visto cómo el carácter no-separable de los sistemas cuánticos ofrece buenos argumentos para sostener una ontología holista o no-local, al menos en el nivel descripto por la mecánica cuántica. Sin duda, esto torna tenues las líneas que delimitan la noción de objeto: ¿qué clase de objeto es aquél que podría extenderse por miles de kilómetros, que no puede ser recuperado una vez que ha interactuado con otro objeto, o cuyas propiedades no pueden explicarse a partir de sus partes constituyentes? No obstante, la mecánica cuántica brinda ulteriores argumentos para desdibujar por completo la noción de objeto, poniendo en cuestión, de manera directa, su individualidad o, en términos más precisos, la posibilidad de utilizar criterios y condiciones de identidad para singularizar sistemas cuánticos.
Desde el punto de vista de la estadística sobre una multiplicidad de sistemas cuánticos, cabe preguntarse qué tipo de individualidad le cabe a los objetos cuánticos, si es que les cabe alguna. La aplicación estadística de la mecánica exigió la introducción de un postulado extra, el postulado de simetrización, de acuerdo con el cual, al tratar con conjuntos de partículas, no podemos considerar a cada una de ellas como individuos satisfaciendo condiciones y criterios de identificación. Veamos cómo esta conclusión es sugerida a partir del formalismo de la mecánica cuántica.
En física es usual utilizar nociones estadísticas para calcular la distribución de probabilidad sobre los estados posibles de múltiples sistemas. Supongamos dos sistemas ![]() y
y ![]() que pueden encontrarse en cualesquiera de dos estados posibles
que pueden encontrarse en cualesquiera de dos estados posibles ![]() y
y ![]() . Si se trata de sistemas y estados clásicos, existen cuatro configuraciones posibles:
. Si se trata de sistemas y estados clásicos, existen cuatro configuraciones posibles:
(a) Ambos sistemas, ![]() y
y ![]() , se encuentran en el estado
, se encuentran en el estado ![]() .
.
(b) Ambos sistemas, ![]() y
y ![]() , se encuentran en el estado
, se encuentran en el estado ![]() .
.
(c) El sistema ![]() se encuentra en
se encuentra en ![]() y el sistema
y el sistema ![]() se encuentra en
se encuentra en ![]() .
.
(d) El sistema ![]() se encuentra en
se encuentra en ![]() y el sistema
y el sistema ![]() se encuentra en
se encuentra en ![]() .
.
A su vez, cuando las cuatro configuraciones son igualmente probables, la probabilidad de que ocurra cada una de ellas es 1/4. Si al realizar las mediciones correspondientes no se obtiene esta distribución, se buscará el factor responsable de introducir una asimetría en la situación bajo estudio.
Si bien razonable en el mundo clásico, esta distribución de probabilidades no se cumple con partículas cuánticas. En el caso en que las partículas son bosones, como los fotones (para fermiones la situación es diferente, pero ello no altera las cuestiones ontológicas), sin ningún factor conocido responsable de asimetrías, la distribución de probabilidades que se obtiene es: 1/3 para la configuración (a), 1/3 para la (b), y 1/3 para la conjunción de las configuraciones (c) y (d). Esto significa que la permutación de los sistemas respecto de sus estados no parece conducir a dos configuraciones distintas: la distribución de probabilidad no distingue entre ![]() en
en ![]() y
y ![]() en
en ![]() por un lado, y
por un lado, y ![]() en
en ![]() y
y ![]() en
en ![]() por el otro como dos casos diferentes.
por el otro como dos casos diferentes.
Desde un punto de vista formal, la situación se aborda del siguiente modo. Si consideramos el estado del sistema compuesto ![]() , éste será
, éste será ![]() en el caso (a) y
en el caso (a) y ![]() en el caso (b). Siguiendo la misma estrategia, el estado
en el caso (b). Siguiendo la misma estrategia, el estado ![]() del sistema
del sistema ![]() correspondería al caso (c), mientras que el estado
correspondería al caso (c), mientras que el estado ![]() correspondería al caso (d). Si esto fuese así, se trataría de estados compuestos distintos, ya que la operación
correspondería al caso (d). Si esto fuese así, se trataría de estados compuestos distintos, ya que la operación ![]() no es conmutativa. Sin embargo, como mencionamos en el párrafo anterior, esto no es lo que se obtiene a partir de la estadística. Es aquí donde ingresa el postulado de simetrización, según el cual en ambos casos el estado es del sistema compuesto
no es conmutativa. Sin embargo, como mencionamos en el párrafo anterior, esto no es lo que se obtiene a partir de la estadística. Es aquí donde ingresa el postulado de simetrización, según el cual en ambos casos el estado es del sistema compuesto ![]() es:
es:
Este estado no distingue entre los casos (c) y (d) y, por tanto, considera ambos como una configuración única. Por ello, se dice que las partículas son indistinguibles. Si bien la utilización del postulado de simetrización funciona correctamente en los cálculos, se trata de una hipótesis completamente ad hoc para dar cuenta de la estadística cuántica. La pregunta ontológica se refiere a cómo justificar la introducción de dicho postulado.
Una primera respuesta consistiría en afirmar que, si bien existen cuatro configuraciones posibles, en realidad no son equiprobables. La estadística cuántica de los bosones se obtendría si las probabilidades de los casos (a) y (b) fueran 1/3 cada una, pero las probabilidades de los casos (c) y (d) fueran 1/6 cada una, de modo que sumadas dieran 1/3 para la conjunción de ambos casos. Si bien lógicamente admisible, esta respuesta no parece plausible desde un punto de vista físico, pues no existe en la mecánica cuántica nada que permita justificar una asimetría como la que requiere la ruptura de equiprobabilidad.
La respuesta tradicional en el marco de la teoría consiste en afirmar que las partículas cuánticas son indistinguibles y, por ello, su permutación no genera una configuración distinta de la original. Sin embargo, es importante considerar qué se entiende por insdistinguibilidad cuántica y cuáles son sus consecuencias respecto de la identidad y la individualidad de las partículas cuánticas.
Supongamos partículas clásicas, como las que conforman un gas. Las partículas nos resultan indistinguibles en un sentido epistémico, ya que no podemos determinar con precisión sus estados clásicos, esto es, sus posiciones y velocidades. Sin embargo, no consideramos que son realmente idénticas ya que, por ejemplo, se distinguen por sus posiciones en el espacio: en un determinado instante, cada partícula tiene una posición precisa diferente a la de cualquiera otra. Si construimos un modelo probabilístico con estas partículas, asumimos sin cuestionamientos que el intercambio de las posiciones de las partículas clásicas (intercambio de sus estados) representa una situación distinta en cada caso. Efectivamente, las partículas podrían ser nombradas y re-identificadas para poder considerar las dos configuraciones resultantes de un intercambio efectivamente como dos configuraciones en lugar de una. En el caso de las partículas cuánticas, el intercambio de partículas no conduce a diferentes configuraciones: la indistinguibilidad no es meramente epistémica, sino que parece adquirir un sentido mucho más profundo, de alcance ontológico. Una situación donde la indistinguibilidad cuántica posee manifestaciones macroscópicas peculiares –como la superfluidez– es el llamado “condensado de Bose-Einstein”: un gas de bosones –partículas de spin entero– enfriado cerca del cero absoluto, donde casi todas las partículas se encuentran en el mismo estado de mínima energía.
En la metafísica tradicional existe un principio denominado principio de identidad de los indiscernibles. El principio, formulado por primera vez por Leibniz en su Discurso de Metafísica (1983 [1686]), afirma que no existen dos objetos individuales que posean exactamente las mismas propiedades o, en otras palabras, si dos objetos individuales tienen todas sus propiedades en común, entonces en realidad no son dos sino que son el mismo objeto. Más allá de la discusión metafísica concreta acerca de la validez del principio o de qué clases de propiedades deben considerarse para no trivializarlo, el principio resulta bastante intuitivo a la hora de lidiar con objetos macroscópicos como planetas, galaxias, moléculas o animales. En el caso cuántico, por el contrario, la exigencia de simetría de estado ante la permutación de partículas parece obligar a pensar en partículas completamente indiscernibles, tal como se discute en el experimento mental de las esferas de Black (Black 1959): dos esferas exactamente iguales en un espacio vacío, ¿en qué sentido son dos y no sólo una? En estos casos se suele hablar de diferencia “sólo número”, esto es, la existencia de dos objetos numéricamente distintos aunque totalmente idénticos en todo lo demás. Pero esto cuestiona abiertamente el principio de identidad de los indiscernibles: o bien esta clase de situaciones constituye un genuino contraejemplo del principio de identidad de los indiscernibles, mostrando que es falso; o bien conduce a introducir modificaciones en la manera de entender el principio en vistas a señalar que en realidad no hay una genuina indistinguibilidad (por ejemplo, introduciendo propiedades impuras, esto es, propiedades relacionales que dependen de la identidad de los relata, como, por ejemplo, encontrarse a 1km de la Torre Eiffel).
Ya en la década de los ‘60, Heinz Post (1963) afirmaba que las partículas cuánticas no pueden ser consideradas individuos, puesto que en algún sentido son “no-individuos”. Paul Teller (1998) abordó el problema en términos de “haecceidad”, es decir, aquello que hace que un objeto sea diferente de los demás de un modo que trasciende todas sus propiedades. Según este autor, la creencia en una haecceidad que cumple el papel de principio de individualidad juega un papel crucial en las perplejidades de la estadística cuántica. Post y Teller son sólo algunos de los muchos autores que consideran que la noción de individuo no encaja en la estructura de la mecánica cuántica (ver también French y Krause 2006, y referencias en dicho trabajo).
No obstante, hay quienes creen que no es forzoso dejar de lado la noción de individuo en la mecánica cuántica. Por ejemplo, Steven French (1998) sostiene que el postulado de simetrización debe entenderse como una restricción sobre el conjunto de estados de un sistema cuántico: los estados no-simétricos son inaccesibles. Sobre esta base, afirma que tal restricción es compatible con la interpretación de las partículas cuánticas como individuos: la estadística cuántica se recupera considerando que los estados no-simétricos, si bien posibles, nunca se actualizan. Sin embargo, dado el carácter ad hoc de la restricción en el contexto de la teoría, Michael Redhead y Paul Teller (1992) insisten en que postular estados inaccesibles equivale a introducir una estructura excedente e injustificada en el formalismo.
Más recientemente, otros autores han intentado recuperar el principio de Leibniz mediante la idea de una distinguibilidad débil (Saunders 2003, 2006): dos objetos son débilmente indistinguibles si coinciden en todas sus propiedades y sólo difieren entre sí debido a una relación irreflexiva, como, por ejemplo, “estar al lado de”. Desde esta perspectiva, las partículas cuánticas son débilmente distinguibles y, con ello, continúan regidas por una versión generalizada del principio de identidad de los indiscernibles. Pero no todos aceptan esta estrategia. Por ejemplo, Steven French y Décio Krause (2006) sostienen que la distinguibilidad débil no puede ser usada como argumento para retener la categoría de individuo pues su propia formulación requiere de dicha categoría (ver también Dieks y Versteegh 2008, Dieks y Lubberdink 2011).
Aún más recientemente se ha recuperado la idea de que las partículas cuánticas son no-individuos, pero ahora dotándola de un contenido propositivo: la ontología cuántica es una ontología de propiedades, sin individuos, donde los sistemas son haces de propiedades carentes de toda individualidad (Lombardi y Castagnino 2008, da Costa y Lombardi 2014, Lombardi y Dieks 2016). Una ventaja adicional de esta visión es que promete ser fácilmente extrapolable a la teoría cuántica de campos.
7 Comentarios finales ↑
A lo largo de esta entrada hemos presentado algunos de los problemas ontológicos de la mecánica cuántica más discutidos en la bibliografía. En general, nuestra exposición ha intentado enfocar las dificultades filosóficas que se presentan a la hora de comprender ciertos fenómenos cuánticos valiéndonos de categorías o principios ontológicos usualmente utilizados o supuestos en la física clásica o, incluso, en nuestra vida cotidiana.
En general los debates en este ámbito podrían leerse a la luz de una persistente tensión, aún sin resolver, entre principios ontológicos clásicos y nuevos fenómenos cuánticos. Estos fenómenos, ¿constituyen una refutación de los principios y categorías tradicionales a partir de los cuales conocemos e interactuamos con el mundo? O, por el contrario, ¿debemos desconfiar del carácter acabado y completo de la mecánica cuántica ya que, precisamente, no se ajusta a esos principios y categorías? ¿Necesitamos un nuevo marco categorial y conceptual para aprehender el mundo descripto por la mecánica cuántica? Y en ese caso, ¿cómo compatibilizar este nuevo marco con los principios y las categorías tradicionales? Como hemos señalado al comienzo de este trabajo, hasta el momento no existe consenso acerca de cómo lograr una visión ontológica unificada y sistemática acerca del mundo de acuerdo con la mecánica cuántica. La incertidumbre se torna aún mayor cuando nos adentramos en otras teorías cuánticas, como la teoría cuántica de campos o la gravedad cuántica, donde incluso algunos de los pocos terrenos firmes con los que contábamos en la mecánica cuántica tradicional pierden su solidez.
8 Bibliografía ↑
Albert, D. 1992. Quantum Mechanics and Experience. Cambridge, Mass: Harvard University Press.
Alder, K. 2002. The Measure of All Things: The Seven-Year Odyssey and Hidden Error That Transformed the World. New York: The Free Press.
Allday, J. 2009. Quantum Reality: Theory and Philosophy. Florida: CRC Press.
Aspect, A., P. Grangier y G. Roger. 1982. “Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities”. Physical Review Letters 49 (2): 91–94.
Ballentine, L. 1970. “The Statistical Interpretation of Quantum Mechanics”. Reviews of Modern Physics 42: 358-381.
Ballentine, L. 1998. Quantum Mechanics: A Modern Approach. Singapore: World Scientific Publishing Company.
Bell, J. 1964. “On the Einstein-Podolsky-Rosen paradox”. Physics 1: 195-200.
Berkovitz, J. 2016. “Action at a Distance in Quantum Mechanics”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta, URL= http://plato.stanford.edu/archives/spr2016/entries/qm-action-distance/
Bene, G. y Dieks, D. 2002. “A Perspectival Version of the Modal Interpretation of Quantum Mechanics and the Origin of Macroscopic Behavior”. Foundations of Physics 32: 645-671.
Black, M. 1952. “The Identity of Indiscernibles”. Mind 61: 153-164.
Bohm, D. 1952. “A Suggested Interpretation of the Quantum Theory in Terms of ‘Hidden’ Variables, I and II”. Physical Review 85: 166-193.
Bohm, D. y Aharonov, Y. 1957. “Discussion of Experimental Proof for the Paradox of Einstein, Rosen and Podolski”. Physical Review 108: 1070–1076.
Bohr, N., 1935. “Quantum Mechanics and Physical Reality”. Nature 136: 1025-1026.
Bohr, N. 1959. “Discussion with Einstein on Epistemological Problems in Atomic Physics”. En Albert Einstein: Philosopher-Scientist, editado por Paul A. Schilpp, 199-241. New York: Harper and Row.
Born, M. (ed.). 1971. The Born-Einstein Letters. New York: Walker.
Bub, J. 1997. Interpreting the Quantum World. Cambridge: Cambrideg University Press.
Cabello, A., J. Estebaranz y G. Garcìa-Alcaine. 1996. “Bell-Kochen-Specker Theorem: A Proof with 18 vectors”. Physics Letters A 212: 183-87.
Carsten, H. 2014. “The Kochen-Specker Theorem”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL = http://plato.stanford.edu/archives/win2014/entries/kochen-specker/
Da Costa, N. y Lombardi, O. 2014. “Quantum Mechanics: Ontology without Individuals”. Foundation of Physics 44: 1246-1257.
Deutsch, D. 1999. “Quantum Theory of Probability and Decisions”. Proceedings of the Royal Society of London A 455: 3129-3137.
Deutsch, D. 2002. “The Structure of the Multiverse”. Proceedings of the Royal Society of London A 458: 2911-2923.
Dirac, P. 1967. The Principles of Quantum Mechanics. Oxford: Clarendon Press (version original de 1930).
Dickson, M. 2007. “Non-Relativistic Quantum Mechanics”. En "Philosophy of Physics", editado por Jeremy Butterfield y John Earman, 275-416. Amsterdam: Elsevier.
Dieks, D. 1989. “Quantum Mechanics without the Projection Postulate and its Realistic Interpretation”. Foundations of Physics 38: 1397-1423.
Dieks, D. 1994. “Modal Interpretation of Quantum Mechanics, Measurements, and Macroscopic Behaviour”. Physical Review A 49: 2290-2300.
Dieks, D. 2010. “Quantum Mechanics, Chance and Modality”. Philosophica 83: 117–137.
Dieks, D. y Lubberdink, A. 2011. “How Classical Particles Emerge from the Quantum World”. Foundations of Physics 41: 1051-1064.
Dieks, D. y Vermaas, P. (eds.). 1998. "The Modal Interpretation of Quantum Mechanics". Dordrecht: Kluwer Academic Publishers.
Dieks, D. y Versteegh, M. 2008. “Identical Quantum Particles and Weak Discernibility”. Foundations of Physics 38: 923-934.
Dummett, M. 1973. Frege: Philosophy of Language. New York: Harper and Row.
Einstein, A., B. Podolsky y N. Rosen. 1935. “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?”. Physical Review 47: 777-780.
Esfeld, M. 2001. Holism in Philosophy of Mind and Philosophy of Physics. Dordrecht: Kluwer Academic Publishers.
Everett, H. 1957. “‘Relative State’ Formulation of Quantum Mechanics”. Reviews of Modern Physics 29: 454-462.
Faye, J. 2014. “Copenhagen Interpretation of Quantum Mechanics”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL = http://plato.stanford.edu/archives/fall2014/entries/qm-copenhagen/
Fine, A. 2014. “The Einstein-Podolsky-Rosen Argument in Quantum Theory”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL = http://plato.stanford.edu/archives/win2014/entries/qt-epr/
Frege, G. 1977. “On Concept and Object”. En Translations from the Philosophical Writings of Gottlob Frege, editado por Peter Geach y Max Black, 192-205. Oxford: Basil Blackwell (original de 1892).
French, S. 1998. “On the Withering Away of Physical Objects”. En Interpreting Bodies. Classical and Quantum Objects in Modern Physics, editado por Elena Castellani, 93-113. Princeton: Princeton University Press.
French, S. y D. Krause. 2006. Identity in Physics: A Historical, Philosophical and Formal Analysis. Oxford: Oxford University Press.
Ghirardi, G. 2016. “Collapse Theories”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL = http://plato.stanford.edu/archives/spr2016/entries/qm-collapse/
Ghirardi, G., A. Rimini y T. Weber. 1986. “Unified Dynamics for Microscopic and Macroscopic Systems”. Physical Review D 34: 470-491.
Greaves, H. 2006. “Probability in the Everett Interpretation”. Philosophy Compass 2: 109-128.
Healey, R. 2016. “Holism and Nonseparability in Physics”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL = [http:// plato.stanford.edu/archives/spr2016/entries/physics-holism/ http:// plato.stanford.edu/archives/spr2016/entries/physics-holism/]
Heisenberg, W. 1927. “Über den anschaulichen Inhalt der quantentheoretischer Kinematic und Mechanik”. Zeitschrift für Physik 43: 172-198 (Versión inglesa: 1983. “The Physical Content of Quantum Kinematics and Mechanics”. En Quantum Theory and Measurement, editado por John Wheeler y Wojciech Zurek, 62-84. Princeton: Princeton University Press).
Heisenberg, W. 1959. Physics and Philosophy. Londres: Allen and Unwin.
Hensen, B., H. Bernien, A. E. Dréau, A. Reiserer, N. Kalb, M.S. Blok, J. Ruitenberg, R.F.L. Vermeulen, R.N. Schouten, C. Abellán, W. Amaya, V. Pruneri, M.W. Mitchell, M. Markham, D.J. Twitchen, D. Elkouss, S. Wehner, T. H. Taminiau y R. Hanson. 2015. “Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres”. Nature 526: 682–686.
Honner, J. 1987. The Description of Nature: Niels Bohr and The Philosophy of Quantum Physics. Oxford: Clarendon Press.
Howard, D. 1985. “Einstein on Locality and Separability”. Studies in History and Philosophy of Science 16: 171-201.
Hughes, R. I. G. 1989. The Structure and Interpretation of Quantum Mechanics. Cambridge: Harvard University Press.
Kant, E. 2007. Crítica de la Razón Pura. Buenos Aires: Colihue (versión original de 1781/1787).
Kochen, S. y E. Specker. 1967. “The Problem of Hidden Variables in Quantum Mechanics”. Journal of Mathematics and Mechanics 17: 59-87.
Kochen, S. 1985. “A New Interpretation of Quantum Mechanics”. En Symposium on the Foundations of Modern Physics 1985, editado por Peter Mittelstaed y Pekka Lahti, 151-169. Singapore: World Scientific.
Krips, H. 2016. “Medición en Mecánica Cuántica”. En Diccionario Interdisciplinar Austral, editado por Claudia Vanney, Ignacio Silva y Juan Francisco Franck. URL= http://dia.austral.edu.ar/Medición_en_mecánica_cuántica
Landau, L. y Lifshitz, E. 1972. Mecánica Cuántica No-Relativista. Barcelona: Reverté.
Lange, M. 2002. An Introduction to the Philosophy of Physics. Oxford: Blackwell Publishing.
Leibniz, G. 1983. Discurso de Metafísica. Buenos Aires: Hyspamérica (Versión original de 1686).
Locke, J. 1999. Ensayo sobre el Entendimiento Humano. México: Fondo de Cultura Económica (versión original de 1690).
Lombardi, O. y M. Castagnino. 2008. “A modal-Hamiltonian Interpretation of Quantum Mechanics”. Studies in History and Philosophy of Modern Physics 39: 380-443.
Lombardi, O., S. Fortin, M. Castagnino y J. S. Ardenghi. 2011. “Compatibility Between Environment-Induced Decoherence and the Modal-Hamiltonian Interpretation of Quantum Mechanics”. Philosophy of Science 78: 1024-1036.
Lombardi, O. y D. Dieks. 2016. “Modal Interpretations of Quantum Mechanics”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL= http://plato.stanford.edu/archives/spr2016/entries/qm-modal/
Lowe, E. 1995. “The Metaphysics of Abstract Objects”. The Journal of Philosophy 92: 509-524.
Maudlin, T. 1994. Quantum Nonlocality and Relativity. Oxford: Blackwell.
Maudlin, T. 1998. “Part and Whole in Quantum Mechanics”. En Interpreting Bodies. Classical and Quantum Objects in Modern Physics, editado por Elena Castellani, 285-307. Princeton: Princeton University Press.
Newton, I. 1993. Principios Matemáticos de Filosofía Natural. Barcelona: Altaya (Versión original de la primera edición 1687).
Pessoa, O. 2005. Conceitos de Física Quantica. San Pablo: Editora Livraría da Física.
Popper, K. 1982. Quantum Theory and the Schism in Physics. London: Hutchinson.
Post, H. 1963. “Individuality and Physics”. Listener 70: 534-537.
Quine, W. 1953. “On What There Is”. En From A Logical Point of View, 1-19. Cambridge, Mass.: Harvard University Press.
Redhead, M. y P. Teller. 1992. “Particle Labels and the Theory of Indistinguishable Particles in Quantum Mechanics”. British Journal for the Philosophy of Science 43: 201-218.
Robinson, H. 2014. “Substance”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL = http://plato.stanford.edu/archives/spr2014/entries/substance/
Saunders, S. 2003. “Physics and Leibniz’s Principles”. En Symmetries in Physics: Philosophical Reflections, editado por Katherine Brading y Elena Castellani, 289-307. Cambridge: Cambridge University Press.
Saunders, S. 2006. “Are Quantum Particles Objects?”. Analysis 66: 52-63.
Schilpp, P.A. 1949. Albert Einstein: Philosopher-Scientist. New York: Harper & Row.
Shankar, R. 1994. Principles of Quantum Mechanics. Berlin: Springer.
Susskind, L. y A. Friedman. 2014. Quantum Mechanics: The Theoretical Minimum. New York: Basic Books.
Tal, E. 2015. “Measurement in Science”. En The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL = http://plato.stanford.edu/archives/sum2015/entries/measurement-science/
Teller, P. 1986. “Relational Holism and Quantum Mechanics”. British Journal for the Philosophy of Science 37: 71-81.
Teller, P. 1998. “Quantum Mechanics and Haecceities”. Interpreting Bodies. Classical and Quantum Objects in Modern Physics, editado por Elena Castellani, 114-141. Princeton: Princeton University Press.
Vaidman, L. 2016. “Many-Worlds Interpretation of Quantum Mechanics”. The Stanford Encyclopedia of Philosophy, editado por Edward N. Zalta. URL = http://plato.stanford.edu/archives/spr2016/entries/qm-manyworlds/
van Fraassen, B. C. 1972. “A Formal Approach to the Philosophy of Science”. En Paradigms and Paradoxes: The Philosophical Challenge of the Quantum Domain, editado por Robert Colodny, 303-366. Pittsburgh: University of Pittsburgh Press.
van Fraassen, B. 1974. “The Einstein-Podolsky-Rosen Paradox”. Synthese 29: 291-309.
van Fraassen, B. 1991. Quantum Mechanics. Oxford: Clarendon Press.
van Frassen, B. 2008. Scientific Representation: Paradoxes of Perspective. Oxford: Oxford University Press.
von Neumann, J. 1932. Mathematische Grundlagen der Quantenmechanik. Berlin: Springer.
Wallace, D. 2012. The Emergent Multiverse: Quantum Theory according to the Everett Interpretation. Oxford: Oxford University Press.
Wetzel, L. 2008. Types and Tokens: An Essay on Universals. Cambridge, Mass.: MIT Press.
9 Cómo Citar ↑
Fortin, Sebastian y López, Cristian. 2016. "Problemas ontológicos de la mecánica cuántica". En Diccionario Interdisciplinar Austral, editado por Claudia E. Vanney, Ignacio Silva y Juan F. Franck. URL=http://dia.austral.edu.ar/Problemas_ontológicos_de_la_mecánica_cuántica
10 Derechos de autor ↑
DERECHOS RESERVADOS Diccionario Interdisciplinar Austral © Instituto de Filosofía - Universidad Austral - Claudia E. Vanney - 2016.
ISSN: 2524-941X
11 Herramientas académicas ↑
Entradas relacionadas
Entrelazamiento cuántico e información
Historias en mecánica cuántica
Interpretaciones de la mecánica cuántica
Medición en mecánica cuántica
Otros recursos en línea
“Quantum mechanics”, Stanford Encyclopedia of Philosophy.
“Holism and non-separability in Physics” Stanford Encyclopedia of Philosophy.
“Copenhaguen interpretation of quantum mechanics” Stanford Encyclopedia of Philosophy.
“Identity and individuality in quantum theory” Stanford Encyclopedia of Philosophy.
“The uncertainty principle” Stanford Encyclopedia of Philosophy.
Archivo de Filosofía de las Ciencias de la Universidad de Pittsburgh
12 Agradecimientos ↑
Los autores agradecen los valiosos comentarios recibidos de los dos evaluadores anónimos de este escrito.
