La lógica es, en general, la disciplina filosófica que estudia la inferencia: qué significa que una conclusión se sigue de unas premisas, qué argumentos son válidos y cuáles no y qué métodos tenemos para distinguirlos. La lógica matemática es matemática en un doble sentido. Se trata, en primer lugar, de un modo de entender la lógica que tiene su origen en un contexto matemático (el desarrollo de geometrías no euclidianas y la crisis de los fundamentos ver la voz DIA: “Filosofía de las Matemáticas” sección 2.2: Formalismo: Hilbert) y, como tal, se desarrolló específicamente para el razonamiento matemático. En segundo lugar, la lógica matemática es matemática también por el empleo de herramientas matemáticas para el análisis del razonamiento. En este sentido, la lógica matemática no sólo tiene como tema las matemáticas sino que ella misma es una parte de las matemáticas.
Contemporáneamente, la mayor parte de los estudios de sobre Lógica (fuera de los estudios de Historia de la Lógica) son “lógica matemática” en el segundo sentido mencionado, por lo que es razonable pensar que el término “lógica matemática” debería reservarse para el primer sentido (la lógica que tiene como objeto los razonamientos y métodos de las matemáticas). Creemos, sin embargo, que el estilo matemático de la lógica contemporánea es un modo de aproximarse al razonamiento, no necesariamente el único ni la última palabra sobre éste. El título de este artículo pretende, de este modo, reconocer la validez de otros tipos de aproximación a la lógica como pueden ser los desarrollos medievales de la lógica aristotélica. Simultáneamente, es necesario reconocer que desde finales del siglo XIX, la lógica matemática ha dado lugar a importantes resultados y ha ocupado un papel destacado en la discusión filosófica.
Teniendo en cuenta el carácter interdisciplinar de este diccionario, hemos tratado de expresar las ideas centrales de la lógica matemática de un modo accesible. Hemos procurado que el artículo sea auto-contenido (exceptuando quizá este párrafo), aunque alguna familiaridad con la lógica sin duda ayudará a la comprensión del texto. También por este motivo hemos puesto restricciones a los temas tratados. Concretamente, durante todo el artículo adoptaremos de modo habitual un punto de vista semántico. Al tratar la lógica clásica (sección 2) consideraremos solamente lenguajes de primer orden con identidad, con funciones de uno y dos argumentos y predicados de uno y dos argumentos. Este lenguaje es suficiente para ilustrar qué es la lógica de primer orden y para introducir teorías aritméticas de las que hablaremos en la sección 3. Cuando expliquemos algunos teoremas (sub-sección 2.5 y sección 3), nos limitaremos a dilucidar su contenido y a dar una idea general sobre su demostración, aportando las referencias para una demostración detallada. Cuando tratemos las lógicas no-clásicas, nos restringiremos al caso proposicional mencionando únicamente algunos ejemplos que ilustren la distinción, dentro de esta clase de lógicas, entre extensión y alternativa a la lógica clásica. La sub-sección 2.5 y la sección 3 son un poco más exigentes desde el punto de vista matemático.
En la sección 1 introduciremos la idea general de consecuencia lógica. De ella se desprenden los distintos apartados que debemos especificar para caracterizar con precisión una lógica (tabla 1). En la sección 2 se desarrolla con cierto detalle qué es la lógica clásica de primer orden, explicando las principales propiedades de esta lógica (sub-sección 2.5). En la sección 3 nos centramos en la matemática como tema de la lógica matemática; particularmente en la estructura de la aritmética (números naturales con la sucesión, suma y multiplicación) y en las posibilidades de representación y axiomatización en un lenguaje de primer orden. La sección 4 trata sobre las lógicas no-clásicas. Veremos un ejemplo concreto de alternativa a la lógica clásica, las lógicas de 3 valores [math]\mathsf{K3}[/math] y [math]\mathsf{LP}[/math], y un ejemplo de extensión de la lógica clásica: la lógica modal.
Hemos procurado distinguir los aspectos técnicos de su explicación informal. Para ello, introducimos en primer lugar las definiciones o resultados seguidas de comentarios que clarifican un aspecto de la definición. Los comentarios están ordenados dentro de cada sección: el primer número corresponde a la sección y el segundo a la posición del comentario dentro de la sección.
Contenido
1 Introducción ↑
Un argumento es un conjunto de enunciados con cierto orden: algunos de los enunciados son las premisas y uno de los enunciados es la conclusión. Decimos informalmente que un argumento es válido (equivalentemente: que la conclusión es consecuencia lógica de las premisas) cuando es imposible que sus premisas sean verdaderas y su conclusión falsa. Por ejemplo,
(1) Si Sócrates es marciano entonces Sócrates invadirá la Tierra
(2) Sócrates es marciano
[math]\therefore[/math]
(3) Sócrates invadirá la Tierra
El argumento es válido porque, aunque su conclusión es falsa y alguna de sus premisas verdaderas, sin embargo, necesariamente si sus premisas fuesen todas verdaderas, la conclusión sería verdadera. O en otras palabras: es imposible que sus premisas sean verdaderas y su conclusión falsa.
Pero, ¿qué significa 'imposible' y 'necesario' en este contexto? Significa que no importa cuál sea la interpretación del vocabulario no-lógico, si las premisas son verdaderas, su conclusión es verdadera. Es decir, para comprobar la validez de un argumento debemos, en primer lugar, formalizar el argumento y, en segundo lugar, comprobar si hay alguna interpretación del vocabulario no-lógico donde las premisas sean verdaderas y la conclusión falsa. Tomando el ejemplo anterior,
(1) Si [math]A[/math] entonces [math]B[/math]
(2) [math]A[/math]
[math]\therefore[/math]
(3) [math]B[/math]
el argumento es válido porque no importa cómo interpretemos [math]A[/math] y [math]B[/math], si las premisas son verdaderas en tal interpretación, la conclusión también es verdadera. O en otras palabras, no hay ninguna interpretación de [math]A[/math] y [math]B[/math] que haga verdaderas a las premisas y falsa a la conclusión.
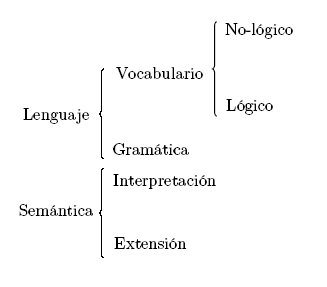
Esta definición de consecuencia lógica muestra que para caracterizar una lógica es necesario describir el lenguaje que estamos empleando, separando el vocabulario lógico del vocabulario no-lógico. Además es necesario explicar en qué consiste una interpretación para el vocabulario no-lógico y cómo, dada una interpretación del vocabulario no-lógico, cualquier fórmula del lenguaje tomará también una interpretación.
2 La lógica clásica de primer orden ↑
Dentro del contexto de la lógica contemporánea se entiende por lógica clásica la lógica descrita de manera completa por primera vez en la obra de Frege de 1879 Begriffsschrift, aunque el término “lógica clásica” se suele restringir a lenguajes de primer orden y en este libro Frege introduce la lógica para lenguajes de segundo orden (ver comentario 2.1 más abajo). Algunas características generales de la lógica clásica son,
- Principio de bivalencia: toda proposición no-ambigua toma un único valor de verdad, verdadero o falso, y al menos uno.
- Extensionalidad: el valor de verdad de una proposición depende exclusivamente de la extensión de sus componentes.
En esta sección describiremos con cierto detalle la lógica clásica de primer orden (sub-secciones 2.1, 2.2 y 2.3), explicaremos de manera algo general qué es un método de demostración (sub-sección 2.4) y explicaremos cuatro teoremas característicos de esta lógica (sub-sección 2.5).
2.1 Lenguaje ↑
El vocabulario no-lógico puede contener:
- Constantes individuales: [math]a_{1}, a_{2}\ldots[/math]
- Símbolos de función de uno o dos argumentos: [math]f_{1}, f_{2}\ldots g_{1}, g_{2}\ldots[/math]
- Símbolos de predicado de uno o dos argumentos: [math]P_{1}, P_{2}\ldots R_{1}, R_{2}\ldots[/math]
Por su parte, el vocabulario lógico contiene:
- Constantes lógicas: [math]\land, \lor, \supset, \lnot[/math]
- Cuantificadores: [math]\forall, \exists[/math]
- Variables individuales: [math]x_1, x_2\dots[/math]
- Identidad: [math]\approx[/math]
- Paréntesis: ( y )
Un término (o término singular) es una expresión del lenguaje que denota un objeto en una interpretación. En los lenguajes de primer orden las constantes y variables individuales son términos. Además, los términos se pueden obtener a partir de símbolos de función y otros términos de acuerdo con la siguiente regla: si [math]t[/math] y [math]u[/math] son términos, entonces [math]f(t)[/math] y [math]g(t,u)[/math] son términos. De modo que [math]f(a_1)[/math] y [math]g(a_3, a_1)[/math] son términos, pero también [math]g(f(a_1), g(a_3, a_1))[/math].
Una fórmula es una expresión del lenguaje que puede ser verdadera o falsa en una interpretación. Si [math]t[/math] y [math]u[/math] son términos y [math]P[/math] y [math]R[/math] son predicados entonces [math]Pt[/math], [math]tRu[/math] y [math]t\approx u[/math] son fórmulas (fórmulas atómicas). Si [math]A[/math] y [math]B[/math] son fórmulas, entonces [math](A\land B)[/math], [math](A\lor B)[/math], [math](A\supset B)[/math], [math]\lnot A[/math], [math]\forall x A[/math] y [math]\exists x A[/math] también son fórmulas. De modo que,
[math]Pg(x, a_1)[/math]
[math]g(a_3, a_1)Rfx[/math] y
[math]g(f(a_1), g(x, a_2))\approx a_5[/math]
son fórmulas, pero también
[math]\exists x((Px\land xRf(a_1))\supset f(a_1)\approx x)[/math]
Comentario 2.1
Un lenguaje proposicional es un lenguaje en el que el vocabulario no-lógico está formado por proposiciones, de manera que puede expresar relaciones lógicas de una proposición con otras proposiciones, pero no relaciones lógicas dentro de una proposición o de una parte de una proposición a otra parte de otra proposición. El argumento en la sección 1 más arriba, se puede formalizar en el lenguaje proposicional de este modo:
(1) Si [math]A\supset B[/math]
(2) [math]A[/math]
[math]\therefore[/math]
(3) [math]B[/math]
(emplearemos el símbolo '[math]\supset[/math]' para el condicional)
Sin embargo, el argumento,
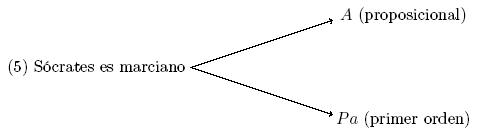
(4) Todos los marcianos invadirán la Tierra
(5) Sócrates es marciano
[math]\therefore[/math]
(6) Sócrates invadirá la Tierra
no tiene una formalización natural al lenguaje proposicional, puesto que la validez del argumento depende de conexiones lógicas entre partes de la proposición (entre los marcianos y el invadir la tierra etc). Un lenguaje de primer orden analiza los elementos que forman la proposición, distinguiendo entre términos y predicados,
Además, en un lenguaje de primer orden podemos realizar generalizaciones sobre la posición de un término. Así, por ejemplo, podemos decir que algún objeto es marciano:
(5[math]^*[/math]) [math]\quad\exists x Px[/math]
En un lenguaje de primer orden no podemos, sin embargo, generalizar sobre la posición de un predicado, diciendo, por ejemplo, que Sócrates tiene alguna propiedad,
(5[math]^{**}[/math]) [math]\quad\exists P Pa[/math]
Esta última fórmula pertenece a un lenguaje de segundo orden (del que no hablaremos más en esta voz).
Comentario 2.2
Los términos de un lenguaje de primer orden pueden ser simples (constantes individuales) o compuestos a partir de funciones. Informalmente, una constante corresponde a un nombre propio, una expresión que sirve para hacer referencia a un objeto, pero que no está compuesta de otras expresiones (por ejemplo `Sócrates'). Informalmente, un término compuesto corresponde a una descripción definida, una expresión que sirve para hacer referencia a un objeto pero que está compuesta de otras expresiones (por ejemplo `el maestro de Platón'). De este modo, podemos formalizar el siguiente tipo de enunciados,
(6) Sócrates es el maestro del maestro de Aristóteles
(7) el maestro de Platón es marciano
[math]\Downarrow[/math]
(6) [math]a_1\approx f_1(f_1(a_2))[/math]
(7) [math]Pf_1(a_3)[/math]
Naturalmente, la lógica de primer orden no fue ideada para hablar de Sócrates, Platón o Aristóteles sino para hablar de números naturales. Bajo esta perspectiva, podemos ver que las afirmaciones aritméticas son, por lo general, afirmaciones de la forma [math]t\approx u[/math] como por ejemplo [math]7\approx 3+(3+3^{0})\cdot 1[/math] (ver la voz DIA: "Filosofía de las Matemáticas", sección 2.2: Formalismo: Hilbert).
Comentario 2.3
Las variables individuales [math]x_1\dots [/math] no tienen, propiamente, un significado, sino que solo sirven para mostrar la posición sobre la que actúan los cuantificadores. Así, por ejemplo, las fórmulas,
(8) [math]\forall y\exists x Ryx[/math]
(9) [math]\forall y\exists x Rxy[/math]
expresan contenidos distintos, igual que las oraciones 'todo el mundo ama a alguien' y 'todo el mundo es amado por alguien'. A la hora de dar una interpretación para el lenguaje, existen distintos modos de tratar las variables. Nosotros las trataremos a casi todos los efectos como constantes individuales.
Comentario 2.4
Las fórmulas de un lenguaje de primer orden son solo un \textit{esquema de oración}, de modo que no son, al margen de una interpretación, ni verdaderas ni falsas. Cuando interpretamos una fórmula es cuando ésta adquiere un valor de verdad. Así, por ejemplo,
(10) [math]aRb[/math]
es verdadera cuando interpretamos '[math]a[/math]' con [math]\mathsf{Bruto}[/math], '[math]b[/math]' con [math]\mathsf{C\acute esar}[/math] y '[math]... R...[/math]' con la relación '[math]...\mathsf{mat\acute o\; a}...[/math]' ; sin embargo cuando interpretamos todo de igual manera excepto '[math]...R...[/math]' que lo interpretamos con la relación '[math]...\mathsf{engendr\acute o\; a}...[/math]' la oración es falsa. Algunas fórmulas son verdaderas en toda interpretación para la lógica clásica, como,
(11) [math]\forall x(Px\supset Px)[/math]
Estas fórmulas se llaman tautologías, o fórmulas válidas. Es habitual, además, distinguir entre oraciones y fórmulas, siendo las primeras fórmulas cuyas variables están todas conectadas con un cuantificador. Una fórmula con alguna variable libre como,
(12) [math]xRa[/math]
se puede entender como un predicado (complejo) en lugar de una oración. Por ejemplo, cuando interpretamos '[math]a[/math]' con [math]\mathsf{Marta}[/math] y '[math]... R...[/math]' con la relación '... [math]\mathsf{es\; hija\; de\;}...[/math]', la fórmula en (12) expresará en predicado '... [math]\mathsf{es\; hija\; de\; Marta}[/math]' (será verdadero de algunos objetos y falso de otros).
Comentario 2.5
Comentario 2.6
Los lenguajes de primer orden comparten el mismo vocabulario lógico (a excepción, quizá, del símbolo de identidad) y pueden diferir en su vocabulario no-lógico. Los símbolos de función y predicados de un lenguaje de primer orden pueden tener cualquier aridad, esto es, cualquier número de argumentos. Por simplicidad nosotros hablaremos únicamente de lenguajes cuyos símbolos de función y predicados tengan, a lo sumo, dos argumentos.
2.2 Semántica ↑
Una interpretación para un lenguaje de primer orden [math]\mathcal{L}[/math] es una estructura [math]\langle\mathbb{U}, \mathbb{I}\rangle[/math] donde [math]\mathbb{U}[/math] es un conjunto no-vacío y [math]\mathbb{I}[/math] una función que empareja,
- [math]\mathbb{I}(a)\in\mathbb{U}[/math] para [math]a[/math] variable o constante de [math]\mathcal{L}[/math],
- [math]\mathbb{I}(f)\in\mathbb{U}\to\mathbb{U}[/math] y [math]\mathbb{I}(f)\in\mathbb{U}^{2}\to\mathbb{U}[/math] para [math]f, g[/math] símbolos de función de [math]\mathcal{L}[/math] de uno y dos argumentos respectivamente,
- [math]\mathbb{I}(P)\subseteq\mathbb{U}[/math] y [math]\mathbb{I}(R)\subseteq\to\mathbb{U}^{2}[/math] para [math]P, R[/math] símbolos de predicado de [math]\mathcal{L}[/math] de uno y dos argumentos respectivamente.
Comentario 2.7
Una interpretación para un lenguaje lógico es, en general, una asignación de significado a cada una de las expresiones del vocabulario no-lógico. En el caso de un lenguaje de primer orden, dentro del vocabulario no-lógico podemos encontrar constantes, símbolos de función y símbolos de predicado. Una interpretación para [math]\mathcal{L}[/math] es un conjunto no vacío [math]\mathbb{U}[/math] y una función [math]\mathbb{I}[/math] que asignará a cada expresión del vocabulario no-lógico de [math]\mathcal{L}[/math] un "objeto" en [math]\mathbb{U}[/math] adecuado a la categoría gramatical de la expresión: elementos de [math]\mathbb{U}[/math] para las constantes y variables, funciones en [math]\mathbb{U}[/math] para los símbolos de función, subconjuntos de [math]\mathbb{U}[/math] para los símbolos de predicado de un argumento, subconjuntos de [math]\mathbb{U}\times\mathbb{U}[/math] (esto es, conjuntos de pares ordenados de elementos de [math]\mathbb{U}[/math]) para los símbolos de predicado de dos argumentos.
Comentario 2.8
La extensión de una constante o variable (similar a un nombre propio) es un individuo en [math]\mathbb{U}[/math]. La extensión de un símbolo de función es una función en [math]\mathbb{U}[/math]. Así, informalmente, la extensión de una constante podría ser el individuo [math]\mathsf{Plat\acute on}[/math] y la extensión de un símbolo de función, la función [math]\mathsf{el\; maestro\; de\; ()}[/math]. De este modo, al componer una función con otro término, el resultado será un individuo en [math]\mathbb{U}[/math].
Comentario 2.9
Los símbolos de predicado de un argumento se interpretan con conjuntos de individuos, pues la extensión de un predicado es el conjunto de objetos que satisfacen ese predicado. Así el predicado '... es humano' tiene como extensión el conjunto de mujeres y hombres. Los símbolos de predicados de dos argumentos (aka símbolos de relación) se interpretan con conjuntos de pares de individuos, pues el "objeto" que satisface un símbolo de relación no es un individuo sino un par de individuos. Así, la relación '... es madre de...' es satisfecha por el par [math]\langle\mathsf{María,\; Jes\acute us}\rangle[/math] pero no por el par [math]\langle\mathsf{Jes\acute us,\; María}\rangle[/math].
Dada una interpretación [math]\langle\mathbb{U,I}\rangle[/math], para un lenguaje de primer orden [math]\mathcal{L}[/math], ésta se extiende a todas las fórmulas de [math]\mathcal{L}[/math] de acuerdo con las siguientes cláusulas,
- [math]\mathbb{I}(f(t))=\mathsf{f}(\mathbb{I}(t))[/math] y [math]\mathbb{I}(g(t, u))=\mathsf{g}(\mathbb{I}(t), \mathbb{I}(u))[/math].
- [math]\mathbb{I}(Pt)=1[/math] si y solo si [math]\mathbb{I}(t)\in\mathbb{I}(P)[/math] y [math]\mathbb{I}(Rtu)=1[/math] si y solo si [math]\langle\mathbb{I}(t), \mathbb{I}(u)\rangle\in\mathbb{I}(R)[/math]
- [math]\mathbb{I}(t\approx u)=1[/math] si y solo si [math]\mathbb{I}(t)=\mathbb{I}(u)[/math].
- [math]\mathbb{I}(A\land B)= 1[/math] si y solo si [math]\mathbb{I}(A)=1[/math] y [math]\mathbb{I}(B)=1[/math]
- [math]\mathbb{I}(A\lor B)= 1[/math] si y solo si [math]\mathbb{I}(A)=1[/math] o [math]\mathbb{I}(B)=1[/math]
- [math]\mathbb{I}(A\supset B)= 1[/math] si y solo si [math]\mathbb{I}(A)=0[/math] o [math]\mathbb{I}(B)=1[/math]
- [math]\mathbb{I}(\forall x A)=1[/math] ssi [math]\mathbb{I}^{\dagger}(A)=1[/math] para todo [math]x[/math]-variante [math]\mathbb{I}^{\dagger}[/math] de [math]\mathbb{I}[/math]
- [math]\mathbb{I}(\exists x A)=1[/math] ssi [math]\mathbb{I}^{\dagger}(A)=1[/math] para al menos un [math]x[/math]-variante [math]\mathbb{I}^{\dagger}[/math] de [math]\mathbb{I}[/math]
Comentario 2.10
La cláusula 1 explica cómo toman su referencia los términos compuestos. Así, por ejemplo, si [math]a[/math] es interpretado con [math]\mathsf{Plat\acute on}[/math] y [math]f[/math] con [math]\mathsf{el\; maestro\; de\; ()}[/math], la interpretación de [math]f(a)[/math] será [math]\mathsf{S\acute ocrates}[/math].
Las cláusulas 2 y 3 explican cómo toman su valor de verdad las oraciones atómicas. La cláusula 2 se refiere a las oraciones formadas por símbolos de predicado. Una oración de este tipo es verdadera cuando el individuo (o par de individuos) con que se interpreta el término pertenece al conjunto con que se interpreta el predicado. Así, por ejemplo, si [math]\mathbb{I}(R)= \mathsf{... es\; esposa\; de...}[/math], [math]\mathbb{I}(a)= \mathsf{Xantipa}[/math] y [math]\mathbb{I}(b)= \mathsf{S\acute ocrates}[/math] entonces [math]\mathbb{I}(aRb)=1[/math] (dado que [math]\langle\mathsf{Xantipa,\; S\acute ocrates}\rangle \in\; \mathsf{... es\; esposa\; de\;...})[/math].
La cláusula 3 se refiere a oraciones que envuelven el predicado especial de identidad. A diferencia del resto de predicados y relaciones, que pueden tomar distintas extensiones en distintas interpretaciones, la relación de identidad tiene un significado fijo (por eso lo consideramos parte del vocabulario lógico). Empleamos el símbolo [math]\approx[/math] para no confundir este predicado de nuestro lenguaje lógico con el símbolo de identidad que empleamos en varias ocasiones en nuestra descripción del lenguaje. En efecto, [math]t\approx u[/math] es verdadero exactamente cuando el objeto denotado por [math]t[/math] es el mismo objeto que el denotado por [math]u[/math]. Así, por ejemplo, si [math]\mathbb{I}(a)= \mathsf{Xantipa}[/math], [math]\mathbb{I}(b)= \mathsf{S\acute ocrates}[/math], y [math]\mathbb{I}(f)= \mathsf{el\; esposo\; de\; ()}[/math], entonces [math]\mathbb{I}(b\approx f(a))=1[/math].
Las cláusulas 4 a 6 explican como toman valores de verdad las oraciones con conectivas lógicas. [math]A\land B[/math] es verdadera cuando ambos miembros de la conjunción son verdaderos, etc. Las cláusulas 7 y 8 se refieren a los cuantificadores universal y existencial respectivamente. Un [math]x[/math]-variante [math]\mathbb{I}^{\dagger}[/math] de una función de interpretación [math]\mathbb{I}[/math] es una función que difiere de [math]\mathbb{I}[/math] en, a lo sumo, el valor que asigna a la variable [math]x[/math]. Si una fórmula [math]A[/math] con [math]x[/math] como única variable libre es verdadera para todo [math]x[/math]-variante, esto significa que la condición expresada por [math]A[/math] es satisfecha por todo objeto en [math]\mathbb{U}[/math]. La definición puede parecer ampulosa, pero de hecho es necesaria para describir correctamente el valor de verdad de las oraciones cuantificadas (nótese, que una oración del lenguaje puede contener muchos cuantificadores, unos bajo el alcance de otros).
Ejemplo 2.11
Sea [math]\mathcal{L}[/math] el lenguaje de primer orden cuyo vocabulario extralógico consta de dos predicados de un argumento [math]P[/math] y [math]Q[/math], un predicado de dos argumentos [math]R[/math], un símbolo de función de un argumento [math]f()[/math] y una constante individual [math]c[/math]. Sea [math]\mathcal{A}[/math] la estructura para [math]\mathcal{L}[/math] tal que [math]\mathbb{U}=\{1, 2, 3, 4\},\; \mathbb{I}(P)=\{1, 2\},\; \mathbb{I}(Q)=\{2, 3\}\;\mathbb{I}(R)=\;\leq,\;\mathbb{I}(f)=[/math] sucesión salvo que [math]f(4)=1[/math] y [math]\mathbb{I}(c)=1[/math]. Determine el valor en [math]\mathcal{A}[/math] de cada una de las siguientes oraciones:
- [math]\forall x(Px\lor Qx)[/math]
- [math]\exists x(Px\land\lnot Qx)[/math]
- [math]\forall x (xRf(x))[/math]
- [math]\forall x (x\not\approx f(f(f(c)))\supset xRf(x))[/math]
- [math]\forall x(Px\supset x\approx c)[/math]
- [math]\exists x(Px\land x\approx c)[/math]
- [math]\exists x(\lnot Px\land f(x)\approx c)[/math]
2.3 Consecuencia lógica ↑
Dado un lenguaje de primer orden [math]\mathcal{L}[/math], una fórmula [math]A[/math] de [math]\mathcal{L}[/math] y un conjunto de fórmulas [math]\Gamma[/math] de [math]\mathcal{L}[/math] diremos que [math]A[/math] es una consecuencia lógica de [math]\Gamma[/math], en símbolos [math]\Gamma\vDash A[/math] cuando,
No hay interpretación [math]\langle\mathbb{U}, \mathbb{I}\rangle[/math] tal que[math]\qquad\qquad\qquad[/math]
[math]\mathbb{I}(B)=1[/math] para todo [math]B\in\Gamma[/math] y [math]\mathbb{I}(A)=0[/math].
Comentario 2.12
Esta definición recoge la idea explicada en la sección 1 según la cual un argumento es válido cuando es imposible que sus premisas sean verdaderas y su conclusión falsa (entendiendo por imposible: no hay interpretación). Una manera equivalente de entender la definición es con la idea de necesaria preservación de verdad: un argumento es válido cuando para toda interpretación del vocabulario no-lógico, si sus premisas son verdaderas, su concusión es también verdadera. Esto es, [math]\Gamma\vDash A[/math] cuando,
Para toda interpretación [math]\langle\mathbb{U}, \mathbb{I}\rangle\qquad\qquad\qquad\qquad\qquad[/math]
Si [math]\mathbb{I}(B)=1[/math] para todo [math]B\in\Gamma[/math] entonces [math]\mathbb{I}(A)=1[/math].
En efecto, esta definición es lógicamente equivalente a la anterior (en lógica clásica).
Ejemplo 2.13
Diga si las siguientes afirmaciones son correctas:
- [math]\forall x(Px\supset Qx), \forall x(Qx\supset Sx)\vDash\forall x(Px\supset Sx)[/math]
- [math]\forall x(Px\supset Qx), Pa\vDash Qa[/math]
- [math]\forall x(Px\supset Qx)\vDash\exists x Qx[/math]
- [math]\forall x(Px\supset Qx), \exists x Px\vDash\exists xQx[/math]
- [math]\exists x\forall y Ryx\vDash \forall y\exists x Ryx[/math]
- [math]\forall x\exists y Ryx\vDash \exists y\forall x Ryx[/math]
- [math]Qa, a\approx b\vDash Qb[/math]
- [math]Qa\land\forall x(Px\supset x\approx a)\vDash Pb\supset Qb[/math]
2.4 Demostraciones ↑
Una demostración de [math]A[/math] a partir de [math]\Gamma[/math], escrito [math]\Gamma\vdash A[/math], es una secuencia finita de afirmaciones de la forma [math]\mathcal{X}\vdash Y[/math] donde cada afirmación de este tipo se puede obtener de las anteriores de acuerdo con las reglas en la tabla 3 y cuya última línea es [math]\Gamma\vdash A[/math].
Comentario 2.14
Además de caracterizar una lógica semánticamente nos gustaría disponer de procedimientos formales (o "sintácticos") para establecer demostraciones. Existen sistemas de demostración de muy distinto tipo. La tabla 3 contiene algunas reglas para construir demostraciones. Las reglas son correctas (respecto a la lógica de primer orden) en el sentido de que sólo nos permitirán demostrar argumentos válidos (esto es, [math]\Gamma\vdash A\Longrightarrow \Gamma\vDash A[/math]). El conjunto de reglas no es completo, es decir, no podemos demostrar todas las afirmaciones de consecuencia correctas, ya que no contiene, por ejemplo, reglas para los cuantificadores o la identidad. En esta sección queremos solamente ilustrar qué es un sistema de demostraciones.
Ejemplo 2.15
[math](A\supset B),\; (B\supset C)\;\vdash\; A\supset C[/math]
Más ejemplos con éste método de demostraciones en (Hedman 2006, c. 3).
2.5 Propiedades de la lógica de primer orden ↑
En esta sección describimos cuatro resultados característicos de la lógica clásica de primer orden.
- Completud Si [math]\Gamma\vDash A[/math] entonces [math]\Gamma\vdash A[/math].
- Compacidad Si [math]\Gamma\vDash A[/math] entonces hay un conjunto finito [math]\Gamma^{*}\subseteq\Gamma[/math], tal que [math]\Gamma^{*}\vDash A[/math].
- Löwenheim-Skolem ascendente Si un conjunto de oraciones [math]\Gamma[/math] tiene un modelo infinito, tiene modelos arbitrariamente grandes.
- Löwenheim-Skolem descendente Si un conjunto de oraciones [math]\Gamma[/math] tiene un modelo infinito, tiene un modelo menor o igual que la cardinalidad del lenguaje de [math]\Gamma[/math].
Comentario 2.16
Que la lógica de primer orden es completa quiere decir que existen sistemas de demostración tales que, no solo nos permiten demostrar un argumento únicamente cuando el argumento es válido (corrección), sino que siempre que un argumento es válido, nuestro sistema nos permitirá construir una demostración.
Corrección y completud son las dos direcciones de la equivalencia,
Aunque las relaciones [math]\vDash[/math] y [math]\vdash[/math] son extensionalmente equivalentes, no son la misma relación. El caso es similar a [math]\mathsf{animal\; con\; riñ\acute on}[/math] y [math]\mathsf{animal\; con\; coraz\acute on}[/math], que son propiedades distintas aunque tengan la misma extensión.
De hecho, la demostración de la completud de la lógica de primer orden no es trivial. La prueba más habitual emplea la construcción de Henkin para demostrar que todo conjunto consistente de oraciones tiene un modelo. Que un conjunto de oraciones [math]\Gamma[/math] es consistente significa que [math]\Gamma\nvdash A\land\lnot A[/math]. Por otra parte, un modelo para [math]\Gamma[/math] es una interpretación que hace verdaderas a todas las oraciones en [math]\Gamma[/math]. La idea central de la prueba muestra cómo cualquier conjunto consistente [math]\Gamma[/math] de oraciones se puede extender a un conjunto [math]\Sigma[/math] que es máximamente consistente y que contiene una instancia para cada generalización existencial en [math]\Sigma[/math]. A partir de este conjunto es posible construir una interpretación que haga a todas las oraciones en [math]\Sigma[/math], y por tanto en [math]\Gamma[/math], verdaderas. Ver Zalabardo 2002, c. 5 y Hedman 2006, 148-151, para detalles sobre la prueba.
Comentario 2.17
La compacidad nos dice que si [math]A[/math] es consecuencia lógica de un conjunto [math]\Gamma[/math] de premisas, entonces [math]A[/math] es consecuencia lógica de un subconjunto finito [math]\Gamma^{*}[/math] de [math]\Gamma[/math]. Si [math]\Gamma[/math] es finito, podría suceder que [math]\Gamma=\Gamma^{*}[/math]. Ahora bien, si [math]\Gamma[/math] es infinito, entonces [math]\Gamma^{*}[/math] es más pequeño y, por tanto, hay muchas premisas en [math]\Gamma[/math] "prescindibles", es decir, de las que no depende la validez del argumento.
La compacidad de la lógica de primer orden es una consecuencia de las propiedades de completud y corrección. Pues supongamos que [math]\Gamma\vDash A[/math]. Por el teorema de completud, sabemos que [math]\Gamma\vdash A[/math]. Ahora bien, dado que las demostraciones son finitas, la demostración emplea a lo sumo un número finito de oraciones [math]\Gamma^{*}\subseteq\Gamma[/math], de modo que [math]\Gamma^{*}\vdash A[/math]. Por la corrección de nuestro sistema de demostración obtenemos [math]\Gamma^{*}\vDash A[/math].
La compacidad es de alguna manera la cara y la cruz de la lógica de primer orden. Es una consecuencia directa del teorema de completud que es, aparentemente, un aspecto positivo de la lógica de primer orden. La compacidad, sin embargo, impone limitaciones acerca de los conceptos que pueden expresarse en un lenguaje de primer orden, como la idea de finitud, y que juegan un papel importante en teorías matemáticas interesantes (ver 3.1). Este hecho muestra uno de los aspectos más interesantes e intrigantes de la lógica matemática: la proporción inversa que existe entre poder expresivo y capacidad de demostración.
Comentario 2.18
Una teoría, en términos generales, es un conjunto consistente de oraciones. La construcción de Henkin garantiza que cualquier teoría de un lenguaje de primer orden tiene un modelo (una interpretación donde todas las oraciones de la teoría son verdaderas). Los teoremas de Löwenheim-Skolem se refieren al tamaño de los modelos, donde el tamaño de un modelo [math]\langle\mathbb{U}, \mathbb{I}\rangle[/math] es el tamaño de su universo [math]\mathbb{U}[/math].
Un conjunto es una colección de elementos y como tal tiene un determinado tamaño. Cuando un conjunto es finito, su tamaño viene expresado por un número natural. Sin embargo, ningún número natural expresa el tamaño de un conjunto infinito, pues lo característico de los números naturales es situarse a una distancia finita de 0. La idea de cardinal es la generalización de la noción de tamaño para conjuntos de cualquier tipo. El cardinal infinito más pequeño es el de los números naturales y suele ser representado como [math]\aleph_0[/math] (escribiremos [math]|\mathbb{N}|=\aleph_0[/math]). Dos conjuntos tienen el mismo cardinal cuando hay una correspondencia biunívoca entre ellos. En este sentido, el conjunto de los números naturales y el conjunto de los números racionales tienen el mismo tamaño, pero el conjunto de los números reales tiene un tamaño mayor (más sobre cardinales en (Zabalardo 2002, c. 6) y (Hedman 2006, 150-163)).
En un lenguaje de primer orden podemos encontrar conjuntos de oraciones que ponen un límite por arriba al tamaño de sus modelos. Por ejemplo, la oración [math]\forall x\forall y\forall z(x\approx y\lor x\approx z)[/math] puede ser verdadera en estructuras que tienen a lo sumo dos elementos. El Teorema de Löwenheim-Skolem ascendente nos dice que un conjunto de oraciones de un lenguaje de primer orden con un modelo infinito no puede poner un límite por arriba a sus modelos. El teorema es una consecuencia directa del Teorema de compacidad (detalles en Zabalardo 2002, 298 y Hedman 2006, 167).
En un lenguaje de primer orden podemos encontrar conjuntos de oraciones que ponen un límite por abajo al tamaño de sus modelos. Por ejemplo, la oración [math]\exists x\exists y\exists z(((x\not\approx y)\land(x\not\approx z))\land (y\not\approx z))[/math] puede ser verdadera en estructuras con al menos tres elementos. La cardinalidad de un lenguaje de primer orden es el tamaño del conjunto de oraciones de ese lenguaje y depende directamente del tamaño del vocabulario no-lógico: si este es contable, la cardinalidad del lenguaje es enumerable, si tiene un cardinal mayor, tal será la cardinalidad del lenguaje. El Teorema de Löwenheim-Skolem descendente nos dice que un conjunto de oraciones de un lenguaje de primer orden no puede poner un límite por abajo a sus modelos mayor que la cardinalidad del lenguaje. Esto significa, por ejemplo, que la teoría axiomática de conjuntos [math]\mathsf{ZF}[/math] tiene modelos contables (este hecho es conocido como Paradoja de Skolem, Zabalardo 2002, 294).
La demostración del Teorema de Löwenheim-Skolem descendente tiene cierta complejidad debido principalmente a que envuelve nociones sobre cardinales infinitos. El teorema consiste en un procedimiento para, dado un conjunto de oraciones [math]\Gamma[/math] y un modelo [math]\langle\mathbb{U}, \mathbb{I}\rangle[/math], "depurar" el universo de la interpretación sin variar el valor de verdad de las oraciones en [math]\Gamma[/math]. El procedimiento requiere mantener la extensión de constantes y funciones, pero tomar únicamente un objeto (un "testigo") de [math]\mathbb{U}[/math] para oraciones existencialmente cuantificadas verdaderas en [math]\langle\mathbb{U}, \mathbb{I}\rangle[/math] (detalles en Zabalardo 2002, 292 y Hedman 2006, 168-170).
3 Representación y axiomatización de la aritmética ↑
Una interpretación [math]\langle\mathbb{U}, \mathbb{I}\rangle[/math] para un lenguaje [math]\mathcal{L}[/math] es una estructura en el sentido matemático de: un conjunto no vacío con funciones y propiedades / relaciones. La aritmética es la estructura (que llamaremos [math]\mathcal{N}[/math]) formada por el conjunto de los números naturales [math]\mathbb{N}[/math], linealmente ordenados por la relación [math]\mathsf{menor\; o\; igual\; que}[/math], con cero como elemento mínimo, sin elemento máximo y con las funciones de sucesión, suma y multiplicación. El lenguaje de la aritmética [math]\mathcal{L}_A\[/math] es un lenguaje de primer orden con identidad similar a esta estructura en el sentido de que contiene una constante, un símbolo de un argumento y dos símbolos de dos argumentos: [math]0, s, +, \cdot[/math] (no confundir expresiones del lenguaje con las funciones en [math]\mathcal{N}[/math]). En la primera sección hablaremos de las posibilidades de representación de [math]\mathcal{N}[/math] con oraciones de [math]\mathcal{L}_A\[/math]. En la sección siguiente hablaremos de las posibilidades de axiomatización de [math]\mathcal{N}[/math] con oraciones de [math]\mathcal{L}_A\[/math].
3.1 Representación ↑
Podemos emplear oraciones de un lenguaje de primer orden para tratar de representar algunos conceptos. Por ejemplo, la oración
[math]\forall x\forall y\forall z((xRy\land yRz)\supset Ryz)[/math]
es verdadera exactamente en aquellas estructuras en que [math]R[/math] es interpretado con una relación transitiva. De modo similar, podemos emplear conjuntos de oraciones para tratar de representar estructuras enteras, donde una estructura es un conjunto no vacío con funciones y relaciones dentro de ese conjunto (lo que venía siendo una interpretación en la sección 2.2). Un conjunto de oraciones [math]\Gamma[/math] representa una estructura [math]\mathcal{A}[/math] cuando la estructura es un modelo de [math]\Gamma[/math]. Por ejemplo, la oración anterior representa las estructuras donde [math]R[/math] es interpretado con una relación transitiva. Sin embargo, esa oración no representa ninguna estructura en particular con gran detalle, puesto que es verdadera en estructuras que son muy distintas entre sí (es verdadera, por ejemplo, tanto en estructuras finitas como estructuras infinitas).
Un isomorfismo de una estructura [math]\mathcal{A}[/math] a una estructura [math]\mathcal{B}[/math] es una función [math]h[/math] del universo de [math]\mathcal{A}[/math] al universo de [math]\mathcal{B}[/math], [math]h:\mathbb{A}\longrightarrow\mathbb{B}[/math], que cumple las siguientes características,
- [math]h[/math] es una correspondencia entre los universos de [math]\mathcal{A}[/math] y [math]\mathcal{B}[/math]
- para cada constante [math]a[/math] de [math]\mathcal{L}[/math], [math]h(a_{\mathcal{A}})=a_{\mathcal{B}}[/math]
- para cada símbolo de función [math]f[/math] de [math]\mathcal{L}[/math] de [math]n[/math] argumentos, [math]h(f_{\mathcal{A}}[a_1\dots a_n])= f_{\mathcal{B}}(h[a_1]\dots h[a_n])[/math]
- para cada símbolo de relación [math]R[/math] de [math]\mathcal{L}[/math] de [math]m[/math] argumentos, [math]\langle a_1\dots a_m\rangle\in R_{\mathcal{A}}[/math] ssi [math]\langle h(a_1)\dots h(a_m)\rangle\in R_{\mathcal{B}}[/math].
Se dice que dos estructuras son isomorfas cuando existe un isomorfismo entre ellas. Desde un punto de vista formal, dos estructuras isomorfas son dos copias idénticas. Pueden diferir en aspectos cualitativos (como el tipo de objetos y relaciones que contienen) pero tienen exactamente el mismo número de objetos (cláusula 1) conectados exactamente del mismo modo por funciones en una y otra estructura (cláusula 3) y relaciones con idéntica extensión en cada universo (cláusula 4). Se dice de estructuras isomorfas que son elementalmente equivalentes.
Los lenguajes de primer orden no pueden discriminar entre estructuras isomorfas en el sentido de que cualquier oración de un lenguaje de primer orden que sea verdadera en una estructura [math]\mathcal{A}[/math] es también verdadera en toda estructura isomorfa con [math]\mathcal{A}[/math]. Se dice que un conjunto de oraciones [math]\Gamma[/math] representa una estructura [math]\mathcal{A}[/math] hasta el isomorfismo cuando tiene a [math]\mathcal{A}[/math] como modelo y cualquier otra estructura representada por [math]\Gamma[/math] es isomorfa con [math]\mathcal{A}[/math] (cuando un conjunto de oraciones representa una estructura hasta el isomorfismo se dice que es una teoría categórica) ¿Es posible representar estructuras hasta el isomorfismo?
Si [math]\mathcal{A}[/math] es una estructura finita (esto es, si su universo [math]\mathbb{A}[/math] es finito) entonces existe un conjunto de oraciones de un lenguaje de primer orden que representa [math]\mathcal{A}[/math] hasta el isomorfismo (Zabalardo 2002, 290). Cuando [math]\mathcal{A}[/math] es una estructura infinita, la situación es radicalmente distinta. Por los teoremas de Löwenheim-Skolem, cualquier conjunto de oraciones que represente a [math]\mathcal{A}[/math] tiene modelos de todas las cardinalidades infinitas mayor o igual que la cardinalidad del lenguaje (naturalmente, si el tamaño del universo de [math]\mathcal{A}[/math] es distinto al tamaño del universo de [math]\mathcal{B}[/math], no puede haber una correspondencia, y por tanto isomorfismo, entre estas estructuras). Esto significa ningún conjunto de oraciones de [math]\mathcal{L_A}[/math] representa la estructura de la aritmética [math]\mathcal{N}[/math] hasta el isomorfismo.
Modelos no-estándar de la aritmética
Es posible aún realizar una pregunta más modesta acerca de la posibilidad de representación de estructuras infinitas y de [math]\mathcal{N}[/math] en particular. Sabemos que si [math]\mathcal{A}[/math] es infinita, ninguna teoría que tenga a [math]\mathcal{A}[/math] como modelo es categórica. Sin embargo, aún podría suceder que la teoría represente a [math]\mathcal{A}[/math] y que cualquier otro modelo de la misma cardinalidad que [math]\mathcal{A}[/math] sea isomorfo con [math]\mathcal{A}[/math]. De este modo, aunque una estructura infinita no sea representable hasta el isomorfismo, aún puede ser representable hasta el isomorfismo en su potencia. ¿Es posible representar la estructura de la aritmética [math]\mathcal{N}[/math] con oraciones de [math]\mathcal{L_A}[/math] hasta el isomorfismo en su potencia?
La respuesta es negativa. Sea [math]Teo(\mathcal{N})[/math] el conjunto de todas las oraciones de [math]\mathcal{L_A}[/math] que son verdaderas en [math]\mathcal{N}[/math], es decir [math]Teo(\mathcal{N})[/math] es LA teoría de [math]\mathcal{N}[/math]. Si algún conjunto de oraciones de [math]\mathcal{L_A}[/math] representa a [math]\mathcal{N}[/math] hasta el isomorfismo en su potencia, [math]Teo(\mathcal{N})[/math] lo hace. En otras palabras: si [math]Teo(\mathcal{N})[/math] no representa a [math]\mathcal{N}[/math] hasta el isomorfismo en su potencia, ninguna teoría formulada en [math]\mathcal{L_A}[/math] lo hace. La imposibilidad de representar a [math]\mathcal{N}[/math] hasta el isomorfismo en su potencia consiste en demostrar que [math]Teo(\mathcal{N})[/math] tiene modelos de igual cardinalidad que [math]\mathcal{N}[/math] pero no isomorfos con [math]\mathcal{N}[/math] (estos modelos se llaman modelos no-estándar de la aritmética).
Un número natural es un objeto que se sitúa a una distancia finita de cero. La característica más notable de los modelos no-estándar es que su universo contiene elementos que se sitúan a una distancia infinita de cero (de hecho, tiene infinitas galaxias de elementos no-estándar densamente ordenadas con la galaxia estándar como elemento mínimo y sin elemento máximo, ver Zabalardo 2002, 307-311). El motivo por el que la teoría de la aritmética [math]Teo(\mathcal{N})[/math] no es capaz de detectar la diferencia entre el modelo estándar y los modelos no-estándar es (en términos muy generales) que un lenguaje de primer orden no es capaz de expresar el concepto de finitud. Este hecho está estrechamente ligado a la compacidad de la lógica de primer orden (ver sección 2.5). La propiedad de compacidad se puede expresar del siguiente modo,
Compacidad Si todo subconjunto finito de [math]\Gamma[/math] tiene un modelo, entonces [math]\Gamma[/math] tiene un modelo.
Ejercicio: mostrar que ambas formulaciones son equivalentes.
Consideremos ahora la siguiente lista de oraciones:
- [math]S_{0}[/math] Hay un número finito de objetos en el universo
- [math]S_{1}[/math] Hay al menos un objeto en el universo
- [math]S_{2}[/math] Hay al menos dos objetos en el universo
- [math]S_{3}[/math] Hay al menos tres objetos en el universo
- [math]\vdots[/math]
Cada subconjunto finito de oraciones de esta lista es verdadero en un universo finito, pero no la lista completa. Hay que notar, además, que todas las oraciones [math]S_i\quad (0\lt i)[/math] se pueden expresar en [math]\mathcal{L_A}[/math]. [math]S_{2}[/math], por ejemplo, es [math]\exists x\;\exists y\; (x\;\not\approx\; y)[/math]. De modo que [math]S_0[/math] no se puede expresar en [math]\mathcal{L_A}[/math] o en cualquier otro lenguaje de primer orden.
La noción de finitud resulta esencial para caracterizar la aritmética; más en particular, resulta esencial para caracterizar la noción de número natural. Un número natural es aquél objeto que puede obtenerse a partir de 0 y de un número finito de aplicaciones de la función sucesor. A pesar de que hay infinitos números naturales, lo característico de cualquier número natural es situarse a una distancia finita de 0.
3.2 Incompletud ↑
En la sección anterior vimos algunas limitaciones a la hora de representar la aritmética a través de un conjunto de oraciones de [math]\mathcal{L_A}[/math]. En esta sección se discute sobre la posibilidad de axiomatizar la teoría de la aritmética. El principal resultado en este sentido es que [math]Teo(\mathcal{N})[/math] no es axiomatizable.
Una teoría axiomática es un conjunto de oraciones de un lenguaje lógico (los axiomas) junto con un conjunto de reglas que nos permite construir demostraciones a partir de los axiomas. Para que una teoría sea propiamente axiomática tiene que ser "efectivamente decible" qué fórmulas del lenguaje son demostrables a partir de los axiomas (ver Smith 20017, 22-3). La Aritmética de Peano es una teoría axiomática en este sentido.
(1) dice que el 0 no es el sucesor de ningún número. (2) dice que números distintos tienen sucesores distintos. (3) y (4) explican cómo reducir la suma a la sucesión y (5) y (6) hacen lo propio con la multiplicación. (7) no es propiamente un axioma sino un esquema de axioma. Supongamos que [math]A[/math] es una fórmula de [math]\mathcal{L_A}[/math] con [math]x[/math] como única variable libre y [math]A[x/t][/math] el resultado de sustituir todas las ocurrencias libres de [math]x[/math] por [math]t[/math]. Entonces (7) puede leerse de esta manera: si el 0 tiene una propiedad [math]A[/math] y esta propiedad se hereda a través de la sucesión, entonces todo número tiene la propiedad [math]A[/math]. (7) se conoce como esquema de inducción. Dentro de las teorías aritméticas en [math]\mathcal{L_A}[/math] que tratan de capturar la esencia de la aritmética, la Aritmética de Peano es un buen candidato.
Se dice que una teoría [math]\mathbf{T}[/math] es consistente cuando no hay ninguna oración [math]A[/math] tal que [math]\mathbf{T}\nvdash A\land\lnot A[/math]. Se dice que [math]\mathbf{T}[/math] es completa cuando para toda oración [math]A[/math] o bien [math]\mathbf{T}\vdash A[/math] o [math]\mathbf{T}\vdash\lnot A[/math]. En lógica clásica las teorías inconsistentes no son interesantes pues a partir de ellas podemos demostrar todas las oraciones del lenguaje. Por otra parte, una teoría completa es interesante porque nos da un veredicto para cada una de las preguntas que podemos formular en su lenguaje. El primer teorema de incompletud establece que si la Aritmética de Peano es consistente, entonces es incompleta.
Primer teorema de incompletud. Si [math]\mathbf{T}[/math] es una teoría aritmética (axiomática) capaz de representar ciertas relaciones y funciones sobre los números naturales entonces, si es [math]\mathbf{T}[/math] es consistente, hay una oración [math]G[/math] de [math]\mathcal{L_A}[/math] tal que [math]\mathbf{T}\nvdash G[/math] y [math]\mathbf{T}\nvdash \lnot G[/math].
La demostración de este teorema es laboriosa y seguramente una de las demostraciones en El Libro de Erdös. La Aritmética de Peano expresa propiedades y relaciones sobre los números naturales, pero Gödel demuestra que hay procedimientos para codificar en números naturales afirmaciones acerca de [math]\mathcal{L_A}[/math] y de la propia Aritmética de Peano. De este modo, Gödel muestra cómo una teoría que sea capaz de expresar cierta cantidad de aritmética, es capaz de realizar afirmaciones acerca de la propia teoría. Particularmente, contiene una fórmula [math]Prov(x)[/math] que es verdadera de los números correspondientes a oraciones demostrables en la Aritmética de Peano. A través de una técnica conocida como diagonalización, muestra que hay una oración [math]G[/math] que es verdadera si y sólo si su número correspondiente no está en [math]Prov(x)[/math]. El teorema no muestra solo que la Aritmética de Peano es (si consistente) incompleta, sino, que es incompletable. Podríamos añadir la oración de Gödel [math]G[/math] como un nuevo axioma para dar lugar a una nueva teoría, [math]\mathbf{AP^1}[/math] (si [math]\mathbf{AP}[/math] es consistente entonces [math]\mathbf{AP^1}[/math] también lo es). El procedimiento de Gödel, sin embargo, nos proporcionaría una nueva oración [math]G_{AP^1}[/math] indecidible en [math]\mathbf{AP^1}[/math]. Podemos seguir añadiendo axiomas indefinidamente; siempre que la adición dé lugar a una teoría axiomática, podremos encontrar una nueva oración de Gödel para la teoría resultante. Este último hecho muestra que no hay una única oración indecidible en la Aritmética de Peano sino una cantidad infinita de ellas.
El primer teorema de incompletud puede resultar más o menos sorprendente. Lo cierto es que su contrario sí que hubiera resultado sorprendente. El lenguaje de la aritmética es menos inocente de lo que puede parecer a primera vista. Consideremos las siguientes abreviaturas:
- [math]div(x, y)=_{df}\;\exists z\;(x\cdot z\approx y)[/math]
- [math]par(x)=_{df}\;\exists y\; (y\not\approx 0 \land y + y\approx x)[/math]
- [math]primo(x)=_{df}\;\forall z\;(div(z, x)\supset z\approx 1\lor z\approx x)\land x\not\approx 1[/math]
- [math]y\gt x =_{df}\;\exists z\;(x+z\approx y\land z\not\approx 0)[/math]
[math]div(x, y)[/math] es verdadera de dos números [math]x[/math] e [math]y[/math] exactamente cuando [math]y[/math] es divisible por [math]x[/math]. De modo similar, las siguientes fórmulas expresan las propiedades de ser par, ser primo y ser menor que.
(CG) [math]\forall x((par(x)\land x\gt 2)\supset\exists y\exists z((primo(y)\land primo(z))\land y+z\approx x))[/math]
No sabemos si la Conjetura de Goldbach es verdadera o falsa, pero si la aritmética fuese axiomatizable, éste y una gran cantidad de problemas que han desafiado las mentes más brillantes durante siglos podrían resolverse de manera mecánica.
Segundo teorema de incompletud. Si AP es consistente entonces no puede demostrar la fórmula [math]\mathsf{cons_{AP}}[/math] que dice que AP es consistente.
4 Lógicas no-clásicas ↑
Se entiende por 'lógica clásica' la lógica de primer orden desarrollada en Frege (1879) e introducida en la sección anterior. Desde los inicios, sin embargo, se cuestionó que la lógica clásica fuera adecuada o suficiente para caracterizar diversos aspectos relacionados con el lenguaje natural, la naturaleza de determinados conceptos e incluso la naturaleza última del mundo. Así, por ejemplo, se cuestionó que el condicional de la lógica clásica recogiera el significado de los condicionales del lenguaje natural (Lewis 1912), que la lógica clásica fuera adecuada para representar el significado de las expresiones vagas (Russell 1923), o compatible con la suposición de que el futuro está abierto (Lukasiewicz 1920). Existe una gran cantidad de lógicas que caen bajo el rótulo de lógicas no-clásicas; en esta sección presentaremos solo dos ejemplos: la lógica modal y la lógica de tres valores.
Hay al menos dos sentidos en los que una lógica puede ser no-clásica: por ser una alternativa a la lógica clásica o por ser una extensión de la lógica clásica. Una alternativa a la lógica clásica es una lógica que emplea el mismo lenguaje que la lógica clásica pero que discrepa con la lógica clásica sobre qué argumentos son válidos (típicamente, rechaza la validez de algunos argumentos clásicamente válidos). Una extensión de la lógica clásica es una lógica que emplea un lenguaje más amplio que la lógica clásica de manera que coincide con la lógica clásica para aquellos argumentos que emplean el lenguaje clásico pero mantiene que hay más expresiones lógicas y, por tanto, más argumentos válidos en el nuevo lenguaje.
4.1 Alternativas a la lógica clásica: tres valores ↑
El lenguaje es igual al de la lógica clásica aunque en esta ocasión nos centraremos en el lenguaje proposicional. Contaremos, por tanto, con un conjunto enumerable de variables proposicionales [math]Var[/math]: [math]\{p, q, r, \dots\}[/math] como vocabulario no-lógico, las constantes lógicas clásicas: [math]\lnot, \land, \lor, \supset, \equiv[/math] y dos paréntesis: '[math]([/math]' y '[math])[/math]'.
Una interpretación clásica para el lenguaje proposicional es una asignación de valores de verdad, verdadero o falso y no ambos, a cada una de las variables del lenguaje. En la semántica de tres valores, una interpretación es una asignación de valores de verdad, verdadero, falso o intermedio a las variables. Es decir, una función del conjunto de variables al conjunto de tres valores de verdad: [math]\mathbb{I}\;:\;Var\longrightarrow\{0, \frac{1}{2}, 1\}[/math].
Dada una interpretación de las variables, ésta se extiende a todas las fórmulas del lenguaje de acuerdo a las siguientes cláusulas:
- [math]\mathbb{I}(A\land B)= min(\mathbb{I}(A), \mathbb{I}(B))[/math]
- [math]\mathbb{I}(A\lor B)= max(\mathbb{I}(A), \mathbb{I}(B))[/math]
- [math]\mathbb{I}(\lnot A)=1 - \mathbb{I}(A)[/math]
- [math]\mathbb{I}(A\supset B)= max(1 - \mathbb{I}(A), \mathbb{I}(B))[/math]
Comentario 4.1
La semántica de tres valores difiere de la semántica clásica solamente en incluir un tercer valor: [math]\frac12[/math]. Una vez que ampliamos el número de valores de verdad hay que explicar cómo este nuevo modo de interpretar se extiende a todas las fórmulas del lenguaje. Las cláusulas señaladas más arriba se conocen como esquema de Kleene fuerte. Existen otros modos de extender una interpretación, pero éste es quizá el más natural. La conjunción entre [math]A[/math] y [math]B[/math] toma como valor el mínimo entre los valores de [math]A[/math] y [math]B[/math]. Por ejemplo, si [math]\mathbb{I}(A)=1[/math] y [math]\mathbb{I}(B)=\frac12[/math] entonces [math]\mathbb{I}(A\land B)=\frac12[/math]. Nótese, que la conjunción funciona al modo clásico para los valores clásicos. De modo similar, la disyunción de [math]A[/math] y [math]B[/math] toma el máximo de los valores entre [math]A[/math] y [math]B[/math]. La negación conecta el valor 1 con el valor 0 y el valor 0 con el valor 1 (igual que en el caso clásico) pero conecta el valor [math]\frac12[/math] con él mismo. La definición del condicional se pueden entender en términos de la disyunción y negación, ya que [math]A\supset B;\equiv\;\lnot A\lor B[/math].
[math]A[/math] es una consecuencia lógica de [math]\Gamma[/math] en [math]\mathsf{LP}[/math], en símbolos [math]\Gamma\vDash_{\mathsf{LP}} A[/math] cuando,
No hay interpretación [math]\mathbb{I}[/math] tal que[math]\qquad\qquad\qquad[/math]
[math]\mathbb{I}(B)\gt 0[/math] para todo [math]B\in\Gamma[/math] y [math]\mathbb{I}(A)=0[/math].
[math]A[/math] es una consecuencia lógica de [math]\Gamma[/math] en [math]\mathsf{K3}[/math], en símbolos [math]\Gamma\vDash_{\mathsf{K3}} A[/math] cuando,
No hay interpretación [math]\mathbb{I}[/math] tal que[math]\qquad\qquad\qquad[/math]
[math]\mathbb{I}(B)=1[/math] para todo [math]B\in\Gamma[/math] y [math]\mathbb{I}(A)\lt 1[/math].
Comentario 4.2
El valor 1 es un modo de ser verdadero y el valor 0 un modo de ser falso, pero ¿cómo debemos leer el valor [math]\frac12[/math]? Si [math]\frac12[/math] es un modo de ser verdadero, entonces hay oraciones que son exclusivamente verdaderas (valor 1), exclusivamente falsas (valor 0) y tanto verdaderas como falsas (valor [math]\frac12[/math]). Si [math]\frac12[/math] es un modo de no ser verdadero, entonces hay oraciones que son verdaderas (valor 1), otras son falsas (valor 0) y otras que no son ni verdaderas ni falsas (valor [math]\frac12[/math]). La lógica [math]\mathsf{LP}[/math] se corresponde con la primera interpretación del valor [math]\frac12[/math] y da lugar a una lógica paraconsistente en el sentido de que de una contradicción no se sigue cualquier cosa,
[math]A\land\lnot A\not\vDash_{\mathsf{LP}} B[/math]
La lógica [math]\mathsf{K3}[/math] se corresponde con la segunda interpretación del valor [math]\frac12[/math] y da lugar a una lógica paracompleta en el sentido de que de la ley de tercero excluso no se sigue de cualquier cosa,
[math]B\not\vDash_{\mathsf{K3}} A\lor\lnot A[/math]
La lógica [math]\mathsf{K3}[/math] es empleada por Kleene (1952) en el contexto de su teoría de funciones recursivas parciales. La lógica [math]\mathsf{LP}[/math] es empleada por Priest (1979) para la paradoja del mentiroso y la paradoja de Russell y defendida desde entonces por Priest en multitud de trabajos. Ver Cobreros (2013) para una introducción a estas lógicas, en relación al problema de la vaguedad.
4.2 Extensiones de la lógica clásica: lógica modal ↑
El lenguaje de la lógica modal incluye, además de las variables proposicionales y las conectivas clásicas, los operadores modales '[math]\Box[/math]' y '[math]\Diamond[/math]' que pueden leerse informalmente como 'es necesario que' y 'es posible que'. Las fórmulas del lenguaje modal tienen este aspecto:
[math]p\qquad\Box\lnot p\qquad \lnot\Box p\land\lnot\Box\lnot p\qquad\lnot\Box(p\supset\Diamond(\lnot q\land\Box s))[/math]
Una interpretación modal (un modelo de Kripke) para el lenguaje anterior es una estructura [math]\langle W, R, \mathbb{I}\rangle[/math] donde [math]W[/math] es un conjunto no-vacío (de "mundos posibles"), [math]R[/math] es una relación en [math]W[/math] y [math]\mathbb{I}[/math] una función que asigna valores de verdad a las variables en cada mundo posible (más formalmente: [math]\mathbb{I}[/math] es una función [math]Var\times W\longrightarrow\{1, 0\}[/math]). Escribiremos [math]\mathbb{I}_{w}(p)=1[/math] para decir que la variable [math]p[/math] toma el valor 1 en el mundo [math]w[/math].
Comentario 4.3
Una interpretación clásica es una asignación de valores de verdad a las variables proposicionales. Esta información, sin embargo, no es suficiente para interpretar las expresiones modales pues el valor de verdad de una oración modal no depende (al menos exclusivamente) del valor de verdad de las oraciones que la componen. Considere el caso,
(1) Wittgenstein es futbolista [math]\quad\mathcal{X}[/math]
(2) Wittgenstein no es humano [math]\quad\mathcal{X}[/math]
Ambas proposiciones son falsas. Por otra parte (dejando de lado cuestiones temporales) las proposiciones,
([math]\Diamond[/math]1) Es posible que Wittgenstein sea futbolista [math]\quad\checkmark[/math]
([math]\Diamond[/math]2) Es posible que Wittgenstein no sea humano [math]\quad\mathcal{X}[/math]
tienen presumiblemente distinto valor de verdad (pues ser humano, a diferencia de ser futbolista, es una propiedad esencial).
En la semántica modal, las oraciones del lenguaje modal son verdaderas o falsas en cada mundo posible. El valor de verdad de una oración no-modal en un mundo [math]w[/math] dependerá directamente del valor de verdad de las oraciones que la componen en [math]w[/math]. El valor de verdad de una oración modal, por el contrario, dependerá no sólo del valor de verdad de las oraciones en [math]w[/math] sino también del valor de verdad de las oraciones en mundos accesibles desde [math]w[/math].
Comentario 4.4
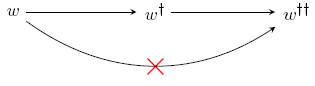
La relación [math]R[/math] de "accesibilidad" entre mundos posibles sirve para representar la idea de posibilidad relativa. En una misma interpretación puede haber mundos [math]w, w^{\dagger}[/math] y [math]w^{\dagger\dagger}[/math] tales que [math]w^{\dagger}[/math] es una posibilidad relativa a [math]w[/math] y [math]w^{\dagger\dagger}[/math] una posibilidad relativa a [math]w^{\dagger}[/math] pero [math]w^{\dagger\dagger}[/math] no es una posibilidad relativa a [math]w[/math]. En forma de gráfico,
Esto permitirá, entre otras cosas, que algo sea necesario pero sólo contingentemente.
Dada una interpretación modal, ésta se extiende a todas las fórmulas del lenguaje de acuerdo con las siguientes cláusulas.
- [math]\mathbb{I}_w(A\land B)=1[/math] si y solo si [math]\mathbb{I}_w(A)=\mathbb{I}_w(B)=1[/math]
- [math]\mathbb{I}_w(A\lor B)=1[/math] si y solo si [math]\mathbb{I}_w(A)=1[/math] o [math]\mathbb{I}_w(B)=1[/math]
- [math]\mathbb{I}_w(A\supset B)=1[/math] si y solo si [math]\mathbb{I}_w(A)=0[/math] o [math]\mathbb{I}_w(B)=1[/math]
- [math]\mathbb{I}_w(\neg A)=1[/math] si y solo si [math]\mathbb{I}_w(A)=0[/math]
- [math]\mathbb{I}_w(\Box A)=1[/math] si y solo si [math]\forall{w^{\dagger}}[/math](si [math]wRw^{\dagger}[/math] entonces [math]\mathbb{I}_{w^{\dagger}}(A)=1)[/math]
- [math]\mathbb{I}_w(\Diamond A)=1[/math] si y solo si [math]\exists_{w^{\dagger}}(wRw^{\dagger}[/math] y [math]\mathbb{I}_{w^{\dagger}}(A)=1)[/math]
Comentario 4.5
Como se apuntó más arriba, las cláusulas muestran que el valor de verdad de una oración no-modal en un mundo [math]w[/math], como [math]A\land B[/math], depende exclusivamente de qué pase con [math]A[/math] y [math]B[/math] en [math]w[/math]. Para que una fórmula de la forma [math]\Diamond A[/math] sea verdadera en [math]w[/math] debe haber al menos un mundo accesible donde [math]A[/math] sea verdadera. Para que [math]\Box A[/math] sea verdadera en [math]w[/math] no debe haber ningún mundo accesible donde [math]A[/math] sea falsa.
[math]A[/math] es una consecuencia lógica de [math]\Gamma[/math], escrito [math]\Gamma\vDash A[/math], cuando
[math]\mathbb{I}_{w}(B)=1[/math] para todo [math]B\in\Gamma[/math] y [math]\mathbb{I}_{w}(A)=0[/math].
Comentario 4.6
Las fórmulas del lenguaje modal son verdaderas o falsas en cada mundo posible. Un contraejemplo a un argumento, por tanto, es una interpretación con un mundo posible donde las premisas son verdaderas y la conclusión falsa. Un argumento es válido cuando no hay contraejemplos. La siguiente inferencia,
(K) [math]\Box (A\supset B)\vDash\Box A\supset\Box B[/math]
es válida de acuerdo con las definiciones anteriores.
Comentario 4.7
La lógica modal que hemos presentado es la más básica de una familia de lógicas conocida como lógicas modales normales. Existen gran cantidad de variaciones de esta lógica que dan lugar a diversos sistemas empleados para representar distintos aspectos del lenguaje como expresiones temporales, condicionales y distintas lecturas de las expresiones modales. Priest (2008) es una comprensiva introducción filosófica a todas estas lógicas (y algunas más).
Comentario 4.8
Aunque la lógica modal es tan antigua como la lógica de Aristóteles, el origen contemporáneo de la lógica modal se puede situar en la obra de Clarence Irvin Lewis (1883-1964), particularmente en Lewis (1912) y en Lewis (1918). La lógica modal se desarrolló, en términos generales, de modo axiomático hasta la obra de Kripke en los años sesenta, donde se generalizó el uso de la semántica modal conocida ahora como "modelos de Kripke". Merece mención también el trabajo de Arthur Prior sobre la lógica y metafísica del tiempo en Prior (1957) y Prior (1967).
5 Lógica, Filosofía y Teología ↑
La Filosofía y la Teología (sobre todo algunas partes, como la teología sistemática) son disciplinas en las que la argumentación juega un papel central. En este sentido, la Lógica (sea matemática o no) resulta un instrumento imprescindible. En esta sección queremos apuntar algunas direcciones en las que la Lógica matemática, la Filosofía y la Teología se han influido recíprocamente, en muchas ocasiones más allá del papel puramente instrumental.
La Lógica matemática ha encontrado muchas aplicaciones fuera del ámbito filosófico, como las matemáticas, la informática teórica, la ingeniería y la lingüística. Una buena parte de resultados lógicos fundamentales tienen, sin embargo, su origen en cuestiones filosóficas. La Conceptografía de Frege (Begriffsschrift) fue escrita con el propósito de esclarecer la naturaleza de las matemáticas y los teoremas de incompletud de Gödel están ligados al intento de Hilbert de fundamentación de las matemáticas. El estudio de las paradojas de la teoría de conjuntos y las paradojas semánticas dio lugar a desarrollos lógicos como las lógicas multivaloradas y a las teorías axiomáticas de conjuntos. El interés por los condicionales del lenguaje natural y, de manera independiente, consideraciones sobre la semántica y metafísica del tiempo, contribuyeron al nacimiento y desarrollo de la lógica modal contemporánea.
A su vez, los resultados lógicos han tenido impacto en cuestiones filosóficas. La visión positivista de la ciencia del Círculo de Viena, por ejemplo, está ligada a los entonces recientes descubrimientos de la lógica matemática. Los teoremas de Löwenheim-Skolem se han empleado (Putnam 1983) para argumentar en contra del realismo en Filosofía del Lenguaje y Metafísica. El Teorema de Tarski (1936) ha tenido una gran influencia sobre los estándares que debe satisfacer cualquier teoría adecuada sobre la verdad.
La Lógica matemática ha tenido también influencia sobre la Teología, al menos sobre la Teología Filosófica. Tiempo después de la muerte de Kurt Gödel, se publicó una reconstrucción que éste hizo del argumento ontológico. El argumento ontológico de Gödel emplea lógica modal de segundo orden (cuantificación sobre propiedades) y se presenta en forma de demostración a partir de un número de axiomas (si los argumentos de autoridad tienen algún valor, resulta difícil dudar de la validez de este argumento). El argumento ontológico modal, así llamado, es reformulado y defendido de manera notable en Plantinga (1974, c. 10).
El propio concepto de Dios, sobre todo en su concepción clásica, desafía la lógica humana. ¿Cómo debemos entender la impecabilidad, la omnipotencia o la omnisciencia divina? Este tipo de cuestiones son objeto de un intenso debate en la contemporánea teología analítica que emplea a menudo los métodos de análisis proporcionados por la lógica matemática. En Cobreros (2016), por ejemplo, se aplica la semántica superevaluacionista para formular de modo preciso la solución eternalista al problema de la presciencia divina y el determinismo. El empleo de la lógica matemática dentro del análisis teológico ha dado lugar, incluso, a debates metateológicos. Concretamente: ¿es posible hablar coherentemente acerca de Dios empleando un lenguaje lógico? (ver Kraal 2011).
La lógica matemática suele tener, al menos aparentemente, un desarrollo menor dentro del estudio de problemas de Teología revelada. Las interacciones fructíferas en las relaciones entre Lógica matemática, Filosofía y Teología natural sugieren que el análisis lógico proporcionado por la Lógica matemática tendrá igualmente influencias positivas sobre los diversos problemas de la Teología revelada.
6 Bibliografía ↑
Cobreros, P. 2013. Logic and Paradoxes. Lesson 2: Vagueness. Universidad de Navarra.
Cobreros, P. 2016. “Supervaluationism and the timeless solution to the foreknowledge problem”. Scientia en Fides 4: 61–75.
Frege, G. 1879. Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle: Verlag von Louis Nebert.
Hedman, S. 2006. A First Course in Logic. Oxford: Oxford University Press.
Hughes, G. y Cresswell, M. 1996. A New Introduction to Modal Logic. London: Routledge.
Kleene, S. 1952. Introduction to Metamathematics. El Cerrito, CA: D. Van Nostrand Company Inc.
Kraal, A. 2011. “Logic and divine simplicity”. Philosophy Compass 6: 282–294.
Lewis, C. I. 1912. “Implication and the algebra of logic”. Mind 21: 522–531.
Lewis, C. I. 1918. A survey of symbolic logic. Vancouver: University of California Press.
Plantinga, A. 1974. The Nature of Necessity. Oxford: Oxford University Press.
Priest, G. 1979. “Logic of paradox”. Journal of Philosophical Logic 8: 219–241.
Priest, G. 2008. An introduction to non-classical logic (2nd ed). Cambridge: Cambridge University Press.
Prior, A. N. 1957. Time and Modality. Oxford: Oxford University Press.
Prior, A. N. 1967. Past, present and future. Oxford: Clarendon Press.
Putnam, H. 1983. “Models and reality”. En Realism and Reason, 1-25. Cambridge: Cambridge University Press.
Russell, B. 1923. “Vagueness”. Australasian Journal of Philosophy and Psychology 1(2): 84-92.
Smith, P. 2007. An introduction to Gödel’s Theorems. Cambridge University Press.
Srivastava, S. 2008. A Course in Mathematical Logic. Berlin: Springer Verlag.
Tarski, A. 1936. “Der wahrheitsbegriff in den formalisierten sprachen”. Studia Philosophica 1: 261–405.
Zalabardo, J. L. 2002. Introducción a la teoría de la lógica. Madrid: Alianza Editorial.
7 Cómo Citar ↑
Cobreros, Pablo. 2017. "Lógica matemática". En Diccionario Interdisciplinar Austral, editado por Claudia E. Vanney, Ignacio Silva y Juan F. Franck. URL=http://dia.austral.edu.ar/Lógica_matemática
8 Derechos de autor ↑
DERECHOS RESERVADOS Diccionario Interdisciplinar Austral © Instituto de Filosofía - Universidad Austral - Claudia E. Vanney - 2017.
ISSN: 2524-941X
Campo que se ocupa de las relaciones entre las expresiones y los ítems designados por tales expresiones.