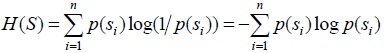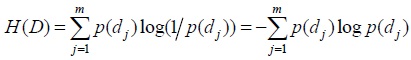(Página creada con «La Teoría de la Información de Claude E. Shannon, es sin duda uno de los avances científicos más importantes del siglo XX. El principal objetivo de esta teoría es el d...») |
|||
| Línea 79: | Línea 79: | ||
<div align="center">I(S;D)= H(S) − E = I(X;Y) = H(D) – N </div> <div align="right">(5)</div> | <div align="center">I(S;D)= H(S) − E = I(X;Y) = H(D) – N </div> <div align="right">(5)</div> | ||
| − | La equivocación E y el ruido ''N ''son medidas de la independencia entre la fuente y el destinatario, dado que si ''S ''y ''D ''son completamente independientes, los valores de E y N son máximos | + | La equivocación E y el ruido ''N'' son medidas de la independencia entre la fuente y el destinatario, dado que si ''S ''y ''D ''son completamente independientes, los valores de E y N son máximos (''E'' = ''H''(''S'') y ''N'' = ''H''(''D'')), y el valor de I(S;D) es mínimo (I(S;D)=0). Por otro lado, si la dependencia entre ''S ''y ''D ''es máxima, los valores de ''E ''y ''N ''son mínimos (''E'' = ''N'' = 0), y el valor de I(S;D) es máximo (I(S;D)=H(S)=H(D)). |
| + | |||
| + | Los valores de E y N son funciones no solo de la fuente y del destinatario, sino también del canal de comunicación CH. La introducción del canal de comunicación lleva directamente a la posibilidad de que se produzcan errores en el proceso de transmisión. El canal CH se puede definir como una matriz [p(d<sub>j</sub>|s<sub>i</sub>)], donde p(d<sub>j</sub>|s<sub>i</sub>) es la probabilidad condicional de ocurrencia de ''d<sub>j</sub>'' en el destinatario dado que ''s<sub>i</sib>'' ocurrió en la fuente ''S''. Los elementos de cada columna de [p(d<sub>j</sub>|s<sub>i</sub>)] suman uno. De este modo, ''E ''y ''N'' se pueden expresar como: | ||
| + | |||
| + | [[File:Shannon 7.jpg|center]] <div align="right">(6)</div> | ||
| + | |||
| + | [[File:Shannon 8.jpg|center]] <div align="right">(7)</div> | ||
| + | |||
| + | donde [[File:Shannon 9.jpg]]. La capacidad del canal C se define como: | ||
| + | |||
| + | [[File:Shannon 10.jpg|center]] <div align="right">(8)</div> | ||
| + | |||
| + | Donde el máximo se toma sobre todas las posibles distribuciones [[File:Shannon 11.jpg]] en la fuente. La magnitud ''C'' se interpreta como la cantidad de información promedio más grande que puede ser transmitida sobre el canal de comunicación ''CH''. | ||
Revisión de 14:14 29 jul 2016
La Teoría de la Información de Claude E. Shannon, es sin duda uno de los avances científicos más importantes del siglo XX. El principal objetivo de esta teoría es el de proporcionar una definición rigurosa de la noción de información que permita cuantificarla. Fue desarrollada con el objetivo de encontrar límites fundamentales en las operaciones de procesamiento de señales tales como compresión de datos, almacenamiento y comunicación. Sus aplicaciones se extienden a campos diversos, entre ellos la física, la química, la biología, la inferencia estadística, la robótica, la criptografía, la computación, la lingüística, el reconocimiento de patrones y la teoría de la comunicación. En esta entrada discutimos los aspectos centrales del formalismo de Shannon y algunos de sus problemas interpretacionales.
Contenido
1 Mundialización e información ↑
El mundo que habitamos hoy, con el incesante desarrollo tecnológico, el aumento considerable de la población mundial y la creciente interacción entre individuos e instituciones de distintas regiones del planeta, ha dado lugar a un aumento sin precedentes en las capacidades de la especie humana para transmitir y procesar información. El ejemplo más conspicuo de esto es quizá el advenimiento de internet, una inmensa red que interconecta a miles de millones de personas en todo el planeta. Esta capacidad para transmitir y procesar información había tenido sus antecesores en el telégrafo, las ondas de radio, el teléfono y otros sistemas de comunicación más antiguos.
Algunos autores, han llegado a afirmar que vivimos en la ‘era de la información’. Independientemente del debate acerca de si esta caracterización histórica es adecuada o no, lo cierto es que el estudio de los problemas técnicos asociados a la transmisión, medición y procesamiento de la información ha cobrado vital importancia para las relaciones sociales y comerciales de la sociedad globalizada. Sin ir más lejos, los mercados actuales dependen fuertemente de que los canales informacionales entre los distintos agentes económicos funcionen en forma fluida y eficiente. Pero la importancia del estudio de los flujos informacionales y su correcto funcionamiento va más allá de la esfera estrictamente económica y abarca fines militares, científicos y recreativos.
En este contexto, el estudio de la Teoría de la Información ha tenido un creciente desarrollo, en el que cada vez más investigadores aúnan esfuerzos para resolver los desafíos planteados por la existencia de unos volúmenes de flujo de información muy difíciles de manejar y administrar. Y es especialmente importante que estos desarrollos contemplen el aspecto matemático formal de la noción de información, de forma tal que ésta se pueda medir y cuantificar para ser aplicada con fines tecnológicos. El desarrollo de una teoría matemática de la información, que permita describir adecuadamente los problemas que los ingenieros comunicacionales encuentran en su trabajo diario es el objetivo que persiguió Claude Shannon cuando desarrolló su formalismo.
Los conceptos y aspectos formales del edificio teórico creado por Shannon siguen siendo explotados y desarrollados en la actualidad. Es por ello que su estudio es de vital importancia para entender el estado actual de la Teoría de la Información, y sus posibles generalizaciones en términos de las florecientes Teorías de la Información Cuántica y de la Computación Cuántica (Duwell 2003; Duwell 2008; Caves y Fuchs 1996; Caves, Fuchs y Schack 2002b; Deutsch y Hayden 2000; Holik, Bosyk y Bellomo 2015; Jozsa 1998; Jozsa 2004; Schumacher 1995; Bub 2005; Clifton; Bub; Halvorson 2003; Nielsen; Chuang 2010; Hayashi 2006).
2 El problema comunicacional y la noción de información ↑
En su artículo ‘A mathematical theory of communication’ (Shannon 1948), Shannon introdujo los lineamientos fundamentales sobre los que se construiría posteriormente la Teoría de la Información. Algunos elementos preliminares de esta teoría habían sido discutidos previamente en la literatura (ver por ejemplo Hartley 1928, Nyquist 1924 y Nyquist 1928). En efecto, al comienzo de su artículo, Shannon señala que:
“El desarrollo de varios métodos de modulación, tales como PCM y PPM que intercambian ancho de banda para una tasa de señal a ruido ha intensificado el interés en una teoría general de la comunicación. Una base para esta teoría está contenida en los importantes artículos de Nyquist y Hartley en este tema. En el presente artículo extenderemos la teoría para incluir un número de nuevos factores, en particular el efecto del ruido en el canal, y los cambios posibles debido a la estructura estadística del mensaje original y debido a la naturaleza final de la destinación de la información.” (Shannon 1948)
Uno de los principales aportes de Shannon fue el especificar cuál es el problema informacional, y separar los aspectos formales de los aspectos semánticos asociados con el contenido del mensaje:
“El problema fundamental de la comunicación es el de reproducir en un punto exacta o aproximadamente un mensaje seleccionado en otro punto. Frecuentemente los mensajes tienen significado; esto es, ellos refieren o están correlacionados de acuerdo a algún sistema con ciertas entidades físicas o conceptuales. Estos aspectos semánticos de la comunicación son irrelevantes para el problema de ingeniería. El aspecto significativo es que el mensaje de hecho es uno seleccionado a partir de un conjunto de posibles mensajes. El sistema debe ser diseñado para operar para cada posible selección, no sólo para aquella que será seleccionada de hecho, dado que es desconocida al momento del diseño.” (Shannon 1948)
De este modo, Shannon define el problema en términos técnicos precisos, separando el problema de ingeniería concreto asociado al proceso de comunicación con los aspectos semánticos de la noción de información vinculados a su uso generalizado en el lenguaje cotidiano. Esto no significa que estos últimos desaparezcan o que no sean importantes; de hecho, los aspectos filosóficos de la Teoría de la Información han dado lugar a importantes debates en la literatura (ver por ejemplo Adriaans 2013; Adriaans y van Benthem, eds. 2008; Bar-Hillel 1964; Bar-Hillel y Carnap 1953; Lombardi 2005; Nauta 1972). Lo que señala Shannon es simplemente que los aspectos semánticos son irrelevantes para el problema planteado en la ingeniería del proceso comunicacional.
El formalismo de Shannon ha sido desarrollado desde diversos enfoques, que poseen un mayor o menor grado de abstracción (ver por ejemplo: Shannon 1943; Shannon 1948; Shannon y Weaver 1949; Cover y Thomas 1991; Khinchin 1957; Reza 1961; Bell 1957). Desde el punto de vista del abordaje Bayesiano a las probabilidades (Cox 1948; Cox 1961), es posible encontrar la medida de Shannon desde una perspectiva alternativa (ver por ejemplo Knuth 2004; Knuth 2005a; Knuth 2005b; Knuth 2012; Goyal y Knuth 2011). Este último enfoque se puede extender a modelos probabilísticos más generales, incluyendo la teoría cuántica y la entropía de von Neumann (Holik, Sáenz, y Plastino 2014; Holik, Plastino, y Sáenz 2016).
Antes de continuar, es importante destacar también que, aparte de la entropía de Shannon, existen otras medidas de la información, como por ejemplo la de Chaitin (1987), la de Fisher (Fisher 1925), y las entropías de Tsallis y Rényi (Rényi 1961; Tsallis 1988; Rastegin 2014; Holik, Bosyk, y Bellomo 2015) que no discutiremos aquí por razones de espacio. Sólo nos limitaremos a decir que estas medidas encuentran numerosas aplicaciones en diferentes contextos, y que tienen una relevancia similar a la de Shannon.
3 El problema de la codificación ↑
Shannon estableció resultados matemáticos acerca de los recursos que se necesitan para la codificación óptima y para la comunicación libre de errores. Estos resultados tuvieron aplicaciones en diversos campos ligados a la teoría de las comunicaciones, como en la radio, la televisión y la telefonía. Hoy en día se siguen aplicando en diversas disciplinas.
De acuerdo a Shannon (1948) (ver también Shannon y Weaver 1949), un sistema de comunicación general consta de varias partes. Una fuente, la cual genera un mensaje a ser recibido en el destinatario. Un transmisor, que transforma el mensaje generado en la fuente en una señal a ser transmitida. En los casos en los que la información es codificada, el proceso de codificación también es implementado por el transmisor. Un canal es cualquier medio que sirva para que la señal se transmita desde el transmisor al receptor. Este puede ser, por ejemplo, un cable, una fibra óptica o una señal inalámbrica. Un receptor, que reconstruye el mensaje a partir de la señal, y finalmente, un destinatario, que es quien recibe el mensaje. En el siguiente dibujo se representan estos elementos en forma esquemática:
La fuente S es un sistema que contiene un conjunto de estados diferentes s1,...,sn, llamados usualmente letras. Un aspecto central de la teoría de Shanonn es que es posible asignar probabilidades de ocurrencia para los distintos estados de la fuente. Es decir, los estados s1,...,sn son producidos con probabilidades p(s1),...,p(sn). Notar que estas distribuciones de probabilidad pueden ser modeladas usando los axiomas de Kolmogorov (Kolmogorov 1933). La cantidad de información generada por la fuente debido a la ocurrencia del estado si se define como:
Dado que S produce sucesiones de estados (estas sucesiones son usualmente llamadas mensajes), la entropía de la fuente S se define como la cantidad promedio de información producida por la fuente:
En forma análoga, el destinatario D es un sistema con un rango de estados posibles d1,...,dm, a los cuales se le asignan probabilidades p(d1),...,p(dm). La cantidad de información I(dj) recibida en el destinatario debido a la ocurrencia de dj se define como:
Y la entropía del destinatario se define como la cantidad promedio de información recibida:
4 Medidas de información ↑
En su artículo original, Shannon (1948, 349) discute la conveniencia del uso de una función logarítmica en la definición de entropías:
“Si el número de mensajes en el conjunto es finito, este número o cualquier función monótona de él puede ser considerado como una medida de la información producida cuando se elije un mensaje del conjunto, siendo todas las opciones igualmente probables. Como fue subrayado por Hartley, la elección más natural es la función logarítmica. Aunque esta definición debe ser generalizada considerablemente cuando consideramos la influencia de la estadística del mensaje y cuando tenemos un rango continuo de mensajes, en todos los casos vamos a usar una medida esencialmente logarítmica.” (Shannon 1948)
Shannon continúa diciendo que esta definición encuentra muchos usos prácticos, dado que muchos parámetros importantes en ingeniería varían linealmente con el logaritmo del número de posibilidades. Señala que es al mismo tiempo una medida intuitiva, porque es usual medir magnitudes comparando linealmente con unidades de medida. Además de estas ventajas, es matemáticamente adecuada dado que resulta ser que muchas operaciones llevadas a cabo con el logaritmo se vuelven mucho más simples que en términos de otras formas funcionales.
La elección de una base logarítmica se corresponderá con la elección de una unidad de medida de la información. Si la base usada es 2, la unidad resultante se llamará ‘bit’. Este término proviene de la contracción del término en inglés ‘bynary digit’. Con estas definiciones, un bit terminará siendo la cantidad de información que se obtiene cuando una de dos alternativas igualmente probables es especificada. En otras palabras, una fuente S con dos estados que puede adoptar los valores 1 y 2 con la misma probabilidad, tendrá una cantidad de información de un bit. Otras bases dan lugar a diferentes unidades de la información. Por ejemplo, si se usan logaritmos naturales, la unidad de medida en este caso será el nat (que es la contracción del término en inglés natural unit). Cuando se usa la base 10 de los logaritmos, la unidad se llama Hartley. La posibilidad de usar diferentes unidades para cuantificar la información muestra la diferencia entre la cantidad de información asociada a un evento y el número de símbolos binarios necesarios para codificarlo. Es importante mencionar que el “bit” es una unidad de medida, y el hecho de que distintas unidades de medida puedan ser usadas no afecta a la naturaleza de la información.
De las definiciones es bastante claro que H(S) y H(D) son cantidades de información promedio. Sin embargo, en la literatura son llamadas usualmente entropías. Efectivamente, la forma funcional que poseen estas medidas de la información, es completamente análoga a las formas funcionales que la entropía adquiere en distintas teorías físicas. Esta terminología refleja una problemática profunda en los fundamentos de la teoría de la información. Esto es así a tal punto que el carácter intrigante de esta magnitud y sus propiedades se manifestó al comienzo de la formulación de la teoría. En efecto, de acuerdo a las palabras mismas de Shannon refiriéndose a cómo llamar a su nueva medida:
“Mi preocupación más grande era cómo llamarla. Pensé en llamarla ‘información’, pero esa palabra estaba muy usada, de forma tal que decidí llamarla ‘incerteza’. Cuando discutí el asunto con John von Neumann, el tuvo una idea mejor. Von Neumann me dijo: ‘Deberías llamarla entropía, por dos motivos. En primer lugar tu función de incerteza ha sido usada en la mecánica estadística bajo ese nombre, y por ello, ya tiene un nombre. En segundo lugar, y lo que es más importante, nadie sabe lo que es la entropía realmente, por ello, en un debate, siempre llevarás ventaja.’” (Tribus and McIrving 1971, 180).
En efecto, la conexión con la física a la que hace mención von Neumann en la cita de arriba ha sido estudiada profundamente en la literatura física y filosófica (ver por ejemplo Landauer 1991; Landauer 1996; Lombardi 2005; Duwell 2003; Duwell 2008; Jozsa 1998; Jozsa 2004; Deutsch y Hayden 2000; Timpson 2003; Timpson 2004; Timpson 2006; Timpson 2008; Timpson 2013; Stonier 1990; Stonier 1996; Floridi 2010; Floridi 2011; Floridi 2013; Brukner y Zeilinger 2001; Brukner y Zeilinger 2009)
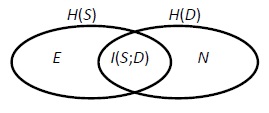
La relación entre las entropías de la fuente H(S) y del destinatario H(D) se puede representar intuitivamente por el siguiente diagrama:
Donde I(S;D) es la información mutua: la cantidad promedio de información generada en la fuente S y recibida en el destinatario D. E es la equivocación: la cantidad promedio de información generada en S pero no recibida en D. N es el ruido: la cantidad promedio de información recibida en D pero no generada en S. Como el diagrama sugiere desde un punto de vista intuitivo, la información mutua se define como:
La equivocación E y el ruido N son medidas de la independencia entre la fuente y el destinatario, dado que si S y D son completamente independientes, los valores de E y N son máximos (E = H(S) y N = H(D)), y el valor de I(S;D) es mínimo (I(S;D)=0). Por otro lado, si la dependencia entre S y D es máxima, los valores de E y N son mínimos (E = N = 0), y el valor de I(S;D) es máximo (I(S;D)=H(S)=H(D)).
Los valores de E y N son funciones no solo de la fuente y del destinatario, sino también del canal de comunicación CH. La introducción del canal de comunicación lleva directamente a la posibilidad de que se produzcan errores en el proceso de transmisión. El canal CH se puede definir como una matriz [p(dj|si)], donde p(dj|si) es la probabilidad condicional de ocurrencia de dj en el destinatario dado que si</sib> ocurrió en la fuente S. Los elementos de cada columna de [p(dj|si)] suman uno. De este modo, E y N se pueden expresar como:
donde ![]() . La capacidad del canal C se define como:
. La capacidad del canal C se define como:
Donde el máximo se toma sobre todas las posibles distribuciones ![]() en la fuente. La magnitud C se interpreta como la cantidad de información promedio más grande que puede ser transmitida sobre el canal de comunicación CH.
en la fuente. La magnitud C se interpreta como la cantidad de información promedio más grande que puede ser transmitida sobre el canal de comunicación CH.