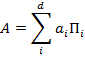| Línea 211: | Línea 211: | ||
===Condiciones de consistencia=== | ===Condiciones de consistencia=== | ||
| − | Hasta aquí hemos hablamos de peso probabilístico sobre historias, y no directamente de probabilidad sobre historias. La razón es que, si bien [[File:4HMQimage015.png]] cumple algunos requisitos mínimos para considerarse una probabilidad, en rigor no los cumple todos, al menos no en todas las posibles familias de historias tal como han sido definidas. Lo que sucede es que, en general, [[File:4HMQimage015.png]] no satisface los axiomas de Kolmogorov para una medida de probabilidad clásica (Mittelstaedt 1998, 74). Lo que falla es que [[File:4HMQimage015.png]] no es aditivo para historias disjuntas (Omnès 1999, 157-160; Griffiths 1984, 224). En términos de los operadores Griffiths esto significa que, si , en general no se cumple que , como se esperaría de una probabilidad bien definida. La única excepción es para historias a dos tiempos; se puede probar que todo conjunto de historias a dos tiempos es consistente, pero un conjunto genérico no lo es (Vanni 2010, 81). | + | Hasta aquí hemos hablamos de peso probabilístico sobre historias, y no directamente de probabilidad sobre historias. La razón es que, si bien [[File:4HMQimage015.png]] cumple algunos requisitos mínimos para considerarse una probabilidad, en rigor no los cumple todos, al menos no en todas las posibles familias de historias tal como han sido definidas. Lo que sucede es que, en general, [[File:4HMQimage015.png]] no satisface los axiomas de Kolmogorov para una medida de probabilidad clásica (Mittelstaedt 1998, 74). Lo que falla es que [[File:4HMQimage015.png]] no es aditivo para historias disjuntas (Omnès 1999, 157-160; Griffiths 1984, 224). En términos de los operadores Griffiths esto significa que, si [[File:5HMQimage002.png]], en general no se cumple que [[File:5HMQimage004.png]], como se esperaría de una probabilidad bien definida. La única excepción es para historias a dos tiempos; se puede probar que todo conjunto de historias a dos tiempos es consistente, pero un conjunto genérico no lo es (Vanni 2010, 81). |
| + | |||
| + | Al efectuar los cálculos explícitos de [[File:5HMQimage006.png]] para historias [[File:5HMQimage007.png]] y [[File:5HMQimage010.png]] cualesquiera dentro de una familia, resulta que siempre aparecen la suma [[File:5HMQimage012.png]] más términos adicionales. Aunque los cálculos generales son algo engorrosos, resultan muy fáciles para historias a tres tiempos (Vanni 2010, 83-84). La idea es buscar familias donde los términos adicionales se anulen, y así [[File:4HMQimage015.png]] pueda considerarse una medida de probabilidad clásica. Esta exigencia se traduce en las llamadas condiciones de consistencia. Se puede demostrar que [[File:4HMQimage015.png]] cumple aditividad dentro de una familia de historias si, para cualquier par de historias disjuntas [[File:5HMQimage007.png]] y [[File:5HMQimage010.png]] en dicha familia, se cumple que | ||
| + | |||
| + | [[File:5HMQimage016.png|center]]<div align="right">(2.9)</div> | ||
| + | |||
| + | Cuando una familia de historias, como las que hemos construido, cumple además esta última condición, se dice que es una'' familia de historias consistentes.'' En ese caso, la familia no sólo forma un contexto de historias cuya estructura lógica es booleana, sino que además está definida una probabilidad que respeta los axiomas de Kolmogorov para una medida de probabilidad clásica. Una familia de historias consistentes se llama también “''framework''” (Griffiths 1996, 2761; 2002, 141). | ||
| + | |||
| + | La ecuación (2.9) es condición necesaria y suficiente para que el peso probabilístico [[File:4HMQimage015.png]] cumpla aditividad dentro de una familia. A veces es llamada ''condición de consistencia de Griffiths'' (Vanni 2010, 85), o ''condición de consistencia débil'' (Griffiths 1996, 2762). Por razones técnicas, a veces es conveniente exigir como condición de consistencia no sólo que la parte real de la expresión en (2.9) se anule, sino que también lo haga la parte imaginaria, con lo cual la condición se convierte en | ||
| + | |||
| + | [[File:5HMQimage018.png|center]]<div align="right">(2.10)</div> | ||
| + | |||
| + | Esta última ecuación (2.10) es condición suficiente, pero no necesaria para que [[File:4HMQimage015.png]] cumpla aditividad dentro de una familia. A veces es llamada condición de consistencia de Gell-Mann y Hartle, ya que fueron quienes la consideraron por primera vez (Gell-Mann y Hartle 1990, 327; 1993, 3353). A veces también es llamada ''condición de consistencia fuerte'' (Griffiths 1996, 2762). | ||
| + | |||
| + | En la formalización de Omnès, si [[File:4HMQimage097.png]] y [[File:4HMQimage100.png]] representan dos historias disjuntas, la condición de consistencia débil adopta la forma | ||
| + | |||
| + | [[File:5HMQimage022.png|center]] | ||
| + | |||
| + | Y de forma análoga, la condición de consistencia fuerte resulta | ||
| + | |||
| + | [[File:5HMQimage024.png|center]] | ||
| + | |||
| + | Como vemos, las condiciones de consistencia, tal como son presentadas por Omnès, quedan en dependencia explicita del estado inicial [[File:5HMQimage026.png]] con el que se prepara al sistema. Esto puede cuestionarse, pues las condiciones que determinan un espacio muestral válido en términos probabilísticos en general quedan definidas previamente a cualquier noción de estado sobre el sistema (Griffiths 1996, 2774; Vanni 2010, 87). Como en las condiciones formuladas por Griffiths no se considera el operador al tiempo inicial como representante de un estado del sistema, éstas parecen más independientes respecto del estado inicial. | ||
| + | |||
| + | Vale la pena enfatizar que, para que una familia [[File:3HMQimage021.png]] sea considerada consistente, las condiciones de consistencia se deben cumplir para todo par de historias disjuntas de la familia. Sin embargo, debido a la linealidad del operador cadena y la traza definida entre operadores, es suficiente que las condiciones de consistencia se cumplan para cualquier par de elementos mínimos [[File:4HMQimage016.png]] distintos que genera la familia, para que toda la familia [[File:3HMQimage021.png]] sea consistente. | ||
| + | |||
| + | |||
| + | ===Refinamiento y compatibilidad=== | ||
| + | |||
| + | Una familia de historias consistentes determina un marco descriptivo de evoluciones de un sistema en términos de propiedades de valor de ciertas magnitudes consideradas. Una vez establecido ese marco, podría desearse refinarlo al incorporar más propiedades que las consideradas en las descripciones. Esto puede lograrse o bien mediante un refinamiento temporal, es decir, agregando más tiempos en las historias con nuevas propiedades a considerar a esos tiempos, o bien con un refinamiento de propiedades a un dado tiempo, es decir, agregando más propiedades al espacio muestral en un tiempo ya dado en la historia. | ||
| + | |||
| + | El ''refinamiento de una familia de historias'' o contexto de historias queda determinado por el refinamiento del espacio muestral que lo genera. En términos de los operadores de Griffiths [[File:3HMQimage081.png]], cualquiera de los dos casos recién mencionados se logra al reemplazar uno o más proyectores en [[File:4HMQimage016.png]] por otros proyectores que, sumados, sean equivalentes a los que se reemplaza. Esta operación incluye el refinamiento temporal, pues cada tiempo adicional que no aparece en [[File:4HMQimage016.png]] puede pensarse representado por el proyector identidad. Por ejemplo, supongamos que tenemos una familia a dos tiempos [[File:4HMQimage032.png]] y [[File:5HMQimage033.png]] determinada por el espacio muestral de historias representadas por el conjunto de los [[File:5HMQimage035.png]], aquí [[File:5HMQimage037.png]]. Para hacer un refinamiento temporal, por ejemplo agregando un tiempo intermedio [[File:5HMQimage034.png]] entre [[File:4HMQimage032.png]] y [[File:5HMQimage033.png]], consideramos que [[File:5HMQimage040.png]]. Así, el refinamiento temporal se logra al efectuar el reemplazo: | ||
| + | |||
| + | <div align="center">[[File:5HMQimage043.png]] siempre que [[File:5HMQimage044.png]]</div> | ||
| + | |||
| + | Por otro lado, un refinamiento de propiedades en un dado tiempo, por ejemplo en el tiempo [[File:4HMQimage032.png]], se logra al efectuar el reemplazo: | ||
| + | |||
| + | <div align="center">[[File:5HMQimage047.png]] siempre que [[File:5HMQimage048.png]]</div> | ||
| + | |||
| + | Se dice que dos familias de historias consistentes ''tienen un refinamiento común'' si existe una tercera familia que las contenga y sea consistente. El refinamiento común más “grueso” entre dos familias, [[File:5HMQimage050.png]] con elementos mínimos [[File:5HMQimage051.png]], y [[File:5HMQimage054.png]] con elementos mínimos [[File:5HMQimage055.png]], es la familia consistente generada por el conjunto de elementos mínimos formados por [[File:5HMQimage058.png]]. Por ejemplo, dadas la familia [[File:5HMQimage050.png]] generada por el conjunto de elementos mínimos [[File:5HMQimage061.png]], y la familia [[File:5HMQimage054.png]] generada por el conjunto de elementos mínimos [[File:5HMQimage064.png]], entonces el refinamiento común más “grueso” es la familia consistente generada por el conjunto de elementos mínimos constituido por [[File:5HMQimage066.png]]. Por supuesto, un refinamiento común entre dos familias será imposible si algún elemento mínimo en una no conmuta con algún elemento mínimo en otra, porque en ese caso ni siquiera se podrá formar un contexto que determine un algebra booleana. Esto nos conduce a la noción de compatibilidad e incompatibilidad entre familias. | ||
| + | |||
| + | Decimos que dos familias son ''compatibles'' si existe un refinamiento común entre ellas, y decimos que son ''incompatibles'' si esto no sucede. Esto implica dos nociones distintas de incompatibilidad entre familias. La primera es la noción habitual de incompatibilidad cuántica, que proviene de considerar propiedades cuyos operadores no conmutan. Si dos operadores de historia no conmutan, no pueden pertenecer a un mismo contexto o familia de historias y, por lo tanto no formarán parte de una estructura lógica clásica. Sin embargo, en el formalismo de historias consistentes, la incompatibilidad puede provenir de una fuente distinta a la falta de conmutatividad. Es posible tener dos familias, cada una consistente por separado, y donde cada uno de los operadores de historia de una familia conmuta con cada uno de los operadores de historia de la otra, pero aun así resultar que no puedan integrarse en una familia más grande que sea consistente. En ese caso la incompatibilidad proviene de la imposibilidad de cumplir las condiciones de consistencia que aseguran una medida de probabilidad válida; por consiguiente, no se puede asegurar la consistencia de razonamientos probabilísticos (en términos de probabilidades condicionales, por ejemplo) que mezclen historias de las distintas familias. En definitiva, la noción de compatibilidad en historias consistentes implica dos aspectos: primero, poder operar con enunciados que formen parte de una estructura booleanas; segundo, poder formular con tales enunciados razonamientos probabilísticos válidos. | ||
| + | |||
| + | Un ejemplo muy instructivo, en el cual existe incompatibilidad debido a la falta de un refinamiento común, es la llamada paradoja de las tres cajas (Griffiths 1996, 2770; 1998, 1616; 2002, 304). Esta paradoja fue inicialmente enunciada por Yakir Aharonov y Lev Vaidman (Aharonov y Vaidman, 1991). Supongamos una partícula que puede estar ubicada en tres cajas [[File:5HMQimage070.png]], [[File:5HMQimage071.png]] o [[File:5HMQimage072.png]]. Cada caja puede concebirse como un estado para la partícula, [[File:5HMQimage076.png]], [[File:5HMQimage077.png]] o [[File:5HMQimage078.png]]. Estos estados deberán ser ortogonales porque son excluyentes, es decir, la presencia en una caja implica ausencia en las otras. Así el sistema puede describirse con un espacio de Hilbert de dimensión tres, donde [[File:5HMQimage076.png]], [[File:5HMQimage077.png]], [[File:5HMQimage078.png]] forman una base. Cada uno de estos estados, por ser estados puros, quedan asociados a las propiedades correspondientes representadas por [[File:5HMQimage079.png]], [[File:5HMQimage081.png]], [[File:5HMQimage083.png]], donde [[File:2HMQimage103.png]] es la identidad del espacio de Hilbert de la partícula. Supongamos un estado inicial para la partícula en el tiempo [[File:2HMQimage063.png]] dado por [[File:5HMQimage090.png]], asociado a la propiedad representada por [[File:5HMQimage092.png]], y un estado final al tiempo [[File:5HMQimage034.png]] dado por [[File:5HMQimage095.png]], asociado a la propiedad representada por [[File:5HMQimage097.png]]. Consideremos ahora dos familias de historias a tres tiempos, con un tiempo intermedio [[File:4HMQimage032.png]]. | ||
| + | |||
| + | Primero consideremos la familia de historias [[File:5HMQimage099.png]] generada por el espacio muestral que determina la descomposición de la identidad [[File:3HMQimage014.png]] en el espacio de historias de la siguiente manera: | ||
Revisión de 17:49 1 sep 2016
La premisa básica del formalismo de historias cuánticas consiste en abandonar la descripción de los sistemas cuánticos en términos de la evolución del estado, regida por la ecuación de Schrödinger. Las evoluciones pasan a ser descriptas en términos de historias, las cuales son entendidas como secuencias estocásticas de propiedades a distintos tiempos. El logro del formalismo es que permite lidiar con las dificultades conceptuales que resultan de la estructura lógica de las propiedades cuánticas, que no respeta la estructura lógica clásica, y a la vez permite desprenderse de la peculiar relación que la interpretación ortodoxa establece entre la evolución del estado cuántico y la asignación de propiedades al sistema en consideración. Si bien el formalismo de historias no puede predecir qué historia se actualizará en el decurso de los eventos, puede determinar condiciones específicas que establecen el conjunto de historias posibles para las propiedades y tiempos considerados. Este conjunto es una suerte de “mapa" de las posibles evoluciones que puede desarrollar el sistema. Dichas evoluciones serán aquéllas que, con una fórmula de la probabilidad previamente definida, cumplan los axiomas de la probabilidad clásica. En términos lógicos, el conjunto de todas las historias posibles determina el universo de discurso del sistema, siendo cada historia considerada como una “proposición elemental de evolución”, es decir, la entidad mínima por medio de la cual es posible describir la dinámica del sistema.
En la presente entrada, en primer lugar presentaremos las bases mínimas necesarias para comprender los aspectos fundamentales de la estructura lógica de las propiedades cuánticas, y luego desarrollaremos dos versiones del formalismo de historias cuánticas: el de Historias Consistentes y el de Historias Contextuales.
1 Estructura de propiedades cuánticas ↑
La utilidad de cualquier teoría física consiste en su capacidad de describir las propiedades de los sistemas que estudia, operando con ellas en algún tipo de estructura lógica. Sólo así se podrá entender, explicar y predecir el comportamiento de esos sistemas. Para lograr esto, la teoría debe ser capaz de incorporar elementos formales capaces de representar dichas propiedades en un marco teórico específico.
Cuando hablamos de propiedades de un sistema, aquí nos estamos refiriendo a propiedades de valor que toman sus magnitudes. Por ejemplo, una magnitud fundamental de cualquier sistema físico es su energía ![]() . Asignar una determinada “propiedad de valor” a la magnitud energía es asignar o establecer un valor, o rango de valores a su energía. Así,
. Asignar una determinada “propiedad de valor” a la magnitud energía es asignar o establecer un valor, o rango de valores a su energía. Así, ![]() “energía igual a 5 ergios”,
“energía igual a 5 ergios”, ![]() “energía entre 5 y 7 ergios”, son ejemplos de propiedades de valor un sistema físico.
“energía entre 5 y 7 ergios”, son ejemplos de propiedades de valor un sistema físico.
La mecánica clásica y la mecánica cuántica poseen diferentes elementos formales, sujetos a diferentes estructuras algebraicas, para representar sus propiedades. Estas diferencias son la base sobre la cual radica gran parte de las dificultades conceptuales encontradas a la hora de compatibilizar ambas teorías. En la física clásica, las propiedades de valor de un sistema pueden representarse por subconjuntos o regiones en el llamado espacio de fases del sistema (Hughes 1989, 58). El estado, por otro lado, se representa con un punto en ese espacio. Una propiedad se verifica en el sistema si el estado, como punto, pertenece a la región que representa la propiedad. Esto determina una particular estructura de propiedades en términos de operaciones entre conjuntos.
En términos lógicos, cada propiedad, o más exactamente, cada clase de propiedades lógicamente equivalentes, se puede identificar con una proposición, la proposición que adjudica la propiedad al sistema (Hughes 1989, 182). Con esta identificación, podemos transformar la estructura de propiedades en una estructura lógica. En el caso clásico esto se logra definiendo los conectivos lógicos de conjunción ![]() , disyunción
, disyunción ![]() , y negación
, y negación ![]() en términos de operaciones de intersección, unión y complemento entre conjuntos respectivamente (Hughes 1989, 181-182; Omnès 1999, 101; Vanni 2010, 36). La estructura lógica de propiedades así establecida responde a un algebra booleana, la cual es en esencia el álgebra que establece las operaciones entre conjuntos (Hughes 1989, 178-184; Bub 1997, 15-22; Boole 2009). En este tipo de estructura es posible además establecer una relación de implicación, de suma importancia para los razonamientos lógicos, que es compatible con la relación de inclusión entre conjuntos y permite una asignación de verdad consistente sobre la estructura lógica (Hughes 1989, 202; Omnès 1992, 347; Omnès 1994, 184-185; Bub 1997, 15-20). Sin embargo, esto último y muchas de las características booleanas de la estructura lógica clásica dejan de ser válidas en la mecánica cuántica. Para comprender este punto, es necesario explicar cómo se describen cuánticamente las magnitudes físicas y sus propiedades de valor.
en términos de operaciones de intersección, unión y complemento entre conjuntos respectivamente (Hughes 1989, 181-182; Omnès 1999, 101; Vanni 2010, 36). La estructura lógica de propiedades así establecida responde a un algebra booleana, la cual es en esencia el álgebra que establece las operaciones entre conjuntos (Hughes 1989, 178-184; Bub 1997, 15-22; Boole 2009). En este tipo de estructura es posible además establecer una relación de implicación, de suma importancia para los razonamientos lógicos, que es compatible con la relación de inclusión entre conjuntos y permite una asignación de verdad consistente sobre la estructura lógica (Hughes 1989, 202; Omnès 1992, 347; Omnès 1994, 184-185; Bub 1997, 15-20). Sin embargo, esto último y muchas de las características booleanas de la estructura lógica clásica dejan de ser válidas en la mecánica cuántica. Para comprender este punto, es necesario explicar cómo se describen cuánticamente las magnitudes físicas y sus propiedades de valor.
En la mecánica cuántica, las magnitudes físicas se representan mediante operadores hermíticos que actúan sobre vectores en el llamado espacio de Hilbert ![]() del sistema (Hughes 1989, 63-65; Ballentine 1990, 2-8; Sakurai 1994, 14-16). Aclaramos aquí que, aunque la magnitud no es el objeto que la representa en la teoría, en este caso un operador, en lo que sigue la identificaremos con el operador. Así diremos “magnitud
del sistema (Hughes 1989, 63-65; Ballentine 1990, 2-8; Sakurai 1994, 14-16). Aclaramos aquí que, aunque la magnitud no es el objeto que la representa en la teoría, en este caso un operador, en lo que sigue la identificaremos con el operador. Así diremos “magnitud ![]() ” y escribiremos el operador correspondiente.
” y escribiremos el operador correspondiente.
Cada espacio de Hilbert ![]() tiene subespacios, que son subconjuntos de
tiene subespacios, que son subconjuntos de ![]() que contienen el vector nulo, y además son cerrados ante sumas y multiplicaciones por un escalar (Hughes 1989, 35). Podemos decir que, en mecánica cuántica, las magnitudes físicas toman valores sobre ciertos subespacios en el espacio de Hilbert del sistema. Esto se puede ver al considerar que, debido a la llamada descomposición espectral (Hughes 1989, 50; Ballentine 1990, 10-11), cualquier operador
que contienen el vector nulo, y además son cerrados ante sumas y multiplicaciones por un escalar (Hughes 1989, 35). Podemos decir que, en mecánica cuántica, las magnitudes físicas toman valores sobre ciertos subespacios en el espacio de Hilbert del sistema. Esto se puede ver al considerar que, debido a la llamada descomposición espectral (Hughes 1989, 50; Ballentine 1990, 10-11), cualquier operador ![]() hermítico en un espacio de Hilbert de dimensión igual a
hermítico en un espacio de Hilbert de dimensión igual a ![]() (suponiendo por simplicidad el caso discreto) se puede escribir de la forma
(suponiendo por simplicidad el caso discreto) se puede escribir de la forma
donde, en la llamada notación de Dirac, los ![]() son operadores proyectores sobre el subespacio
son operadores proyectores sobre el subespacio ![]() de dimensión uno (rectas) generado por el vector
de dimensión uno (rectas) generado por el vector ![]() (Hughes 1989, 64). El conjunto de los
(Hughes 1989, 64). El conjunto de los ![]() forman una base ortonormal del espacio de Hilbert (Ballentine 1990, 9: Sakurai 1994 18-19), y cada vector
forman una base ortonormal del espacio de Hilbert (Ballentine 1990, 9: Sakurai 1994 18-19), y cada vector ![]() es llamado autovector de
es llamado autovector de ![]() . Por otro lado, el conjunto
. Por otro lado, el conjunto ![]() es un conjunto de números reales (parametrizados discretamente por el índice
es un conjunto de números reales (parametrizados discretamente por el índice ![]() ) llamado espectro de
) llamado espectro de ![]() , y cada valor
, y cada valor ![]() es llamado autovalor de
es llamado autovalor de ![]() (Hughes 1989, 42-43; Ballentine 1990, 8; Sakurai 1994, 17-19). A veces también se menciona a los
(Hughes 1989, 42-43; Ballentine 1990, 8; Sakurai 1994, 17-19). A veces también se menciona a los ![]() como autoproyectores de
como autoproyectores de ![]() . Como el conjunto de los
. Como el conjunto de los ![]() son ortonormales, los autoproyectores
son ortonormales, los autoproyectores ![]() correspondientes resultan ser ortogonales: esto significa que
correspondientes resultan ser ortogonales: esto significa que ![]() , donde el símbolo
, donde el símbolo ![]() es igual a 1 si
es igual a 1 si ![]() , y es 0 en caso contrario.
, y es 0 en caso contrario.
Haciendo uso de la expresión de ![]() (1.1), es muy fácil ver que
(1.1), es muy fácil ver que ![]() (Sakurai 1994, 17). Así decimos que la magnitud
(Sakurai 1994, 17). Así decimos que la magnitud ![]() toma valor
toma valor ![]() sobre el subespacio
sobre el subespacio ![]() generado por
generado por ![]() porque al aplicar
porque al aplicar ![]() sobre
sobre ![]() , nos devuelve simplemente el valor
, nos devuelve simplemente el valor ![]() multiplicado por
multiplicado por ![]() . Así, los distintos valores
. Así, los distintos valores ![]() que participan en la descomposición espectral son los posibles valores que puede tomar la magnitud
que participan en la descomposición espectral son los posibles valores que puede tomar la magnitud ![]() , los cuales pueden ser corroborados en una medición de dicha magnitud (Hughes 1989, 64). Lo central aquí es que cada posible valor de
, los cuales pueden ser corroborados en una medición de dicha magnitud (Hughes 1989, 64). Lo central aquí es que cada posible valor de ![]() queda naturalmente asociado al subespacio
queda naturalmente asociado al subespacio ![]() y, por lo tanto, al proyector
y, por lo tanto, al proyector ![]() que proyecta sobre
que proyecta sobre ![]() . Debido a esta asociación, las propiedades que asignan un valor, o rango de valores, a la magnitud
. Debido a esta asociación, las propiedades que asignan un valor, o rango de valores, a la magnitud ![]() pueden ser representadas por el proyector asociado a ese valor, o rango de valores. Por ejemplo, la propiedad
pueden ser representadas por el proyector asociado a ese valor, o rango de valores. Por ejemplo, la propiedad ![]() "
"![]() con valor igual a 5” se podrá representar por el proyector
con valor igual a 5” se podrá representar por el proyector ![]() . En cambio, la propiedad
. En cambio, la propiedad ![]() "
"![]() con valor mayor o igual a 5 y menor o igual que 7”, se representará por el proyector
con valor mayor o igual a 5 y menor o igual que 7”, se representará por el proyector ![]() . Como hemos dicho, cada proyector se corresponde con un subespacio en el espacio de Hilbert, por lo que también podemos representar cada propiedad como un subespacio. Esto es de hecho lo que en general se hace en la bibliografía. Aquí, sin embargo, orientados a lo que el formalismo de historias cuánticas necesita, buscaremos tratar las propiedades principalmente en términos de proyectores.
. Como hemos dicho, cada proyector se corresponde con un subespacio en el espacio de Hilbert, por lo que también podemos representar cada propiedad como un subespacio. Esto es de hecho lo que en general se hace en la bibliografía. Aquí, sin embargo, orientados a lo que el formalismo de historias cuánticas necesita, buscaremos tratar las propiedades principalmente en términos de proyectores.
Entre las distintas propiedades que pueden predicarse, existen dos muy particulares: la propiedad universal, también llamada identidad ![]() , que siempre podrá asignarse al sistema; y la propiedad nula, también llamada cero
, que siempre podrá asignarse al sistema; y la propiedad nula, también llamada cero ![]() , que nunca podrá asignarse al sistema. Identificaremos la propiedad universal
, que nunca podrá asignarse al sistema. Identificaremos la propiedad universal ![]() con el proyector identidad en el espacio de Hilbert del sistema, que es el operador que, aplicado a cualquier vector, lo deja idéntico. Es muy útil representar este operador por la suma de todos los posibles autoproyectores asociados a una magnitud dada, es decir
con el proyector identidad en el espacio de Hilbert del sistema, que es el operador que, aplicado a cualquier vector, lo deja idéntico. Es muy útil representar este operador por la suma de todos los posibles autoproyectores asociados a una magnitud dada, es decir ![]() (Ballentine 1990, 10; Sakurai 1994, 19). Sin embargo esa representación no es única; volveremos a esta cuestión más abajo, con la importante noción de espacio muestral. Por otro lado, la propiedad nula se podrá representar por el proyector nulo del espacio de Hilbert del sistema, es decir por el
(Ballentine 1990, 10; Sakurai 1994, 19). Sin embargo esa representación no es única; volveremos a esta cuestión más abajo, con la importante noción de espacio muestral. Por otro lado, la propiedad nula se podrá representar por el proyector nulo del espacio de Hilbert del sistema, es decir por el ![]() visto como operador, que transforma cualquier vector en el vector nulo (Hughes 1989, 15).
visto como operador, que transforma cualquier vector en el vector nulo (Hughes 1989, 15).
Dentro del espacio de Hilbert se pueden definir tres operaciones básicas entre subespacios, que dan como resultado otro subespacio: la intersección, la suma, y el complemento ortogonal de subespacios (Hughes 1989, 190-191; Vanni y Laura 2008; Vanni 2010). Con el conjunto de todos los subespacios del espacio de Hilbert y estas operaciones, queda definida una estructura de propiedades cuánticas, la cual en este caso no resulta booleana (Mittelstaedt 1978, 27; Hughes 1989, 201-206; Bub 1997, 22-30; Vanni 2010).
Como en el caso clásico, es posible identificar clases de propiedades lógicamente equivalentes con proposiciones, y así derivar de la estructura de propiedades una estructura lógica, donde los conectivos conjunción ![]() , disyunción
, disyunción ![]() , y negación
, y negación ![]() se corresponden ahora con las operaciones de intersección, suma, y complemento ortogonal, respectivamente. El álgebra de la estructura lógica cuántica resulta no ser booleana. Adicionalmente, no es posible representar una relación de inferencia lógica asociada a la inclusión de subespacios, como uno esperaría de su análogo clásico: debido a la pérdida de características booleanas, en el caso cuántico no es posible definir una implicación compatible con una asignación de verdad consistente (Hughes 1989, 206; Omnès 1994, 185). Bajo esta limitación, muchas veces las inferencias en mecánica cuántica son elaboradas en función de probabilidades extremas 0 o 1 (Omnès 1994, 157, Omnès 1998, 142).
se corresponden ahora con las operaciones de intersección, suma, y complemento ortogonal, respectivamente. El álgebra de la estructura lógica cuántica resulta no ser booleana. Adicionalmente, no es posible representar una relación de inferencia lógica asociada a la inclusión de subespacios, como uno esperaría de su análogo clásico: debido a la pérdida de características booleanas, en el caso cuántico no es posible definir una implicación compatible con una asignación de verdad consistente (Hughes 1989, 206; Omnès 1994, 185). Bajo esta limitación, muchas veces las inferencias en mecánica cuántica son elaboradas en función de probabilidades extremas 0 o 1 (Omnès 1994, 157, Omnès 1998, 142).
Como estamos interesados en representar a las propiedades en términos de proyectores y no en términos de sus correspondientes subespacios, debemos encontrar qué operaciones entre proyectores corresponden a las operaciones lógicas mencionadas. Antes de proseguir, sin embargo, es necesaria una aclaración respecto de las operaciones posibles entre propiedades incompatibles. En mecánica cuántica, dos magnitudes ![]() y
y ![]() se dicen incompatibles si sus correspondientes operadores no conmutan, esto es, si su conmutador no es nulo (Sakurai 1994, 29). El conmutador entre
se dicen incompatibles si sus correspondientes operadores no conmutan, esto es, si su conmutador no es nulo (Sakurai 1994, 29). El conmutador entre ![]() y
y ![]() se define como
se define como ![]() . Si dos magnitudes son incompatibles, cumplen una relación de incerteza y, por consiguiente no es posible predicar sus propiedades de valor de modo simultáneo, es decir, como conjunciones (Ballentine 1990, 183; Sakurai 1994, 35). La postura tradicional consiste en sostener que las conjunciones tienen sentido sólo si corresponden a magnitudes compatibles. Esta es la postura adoptada en el formalismo de historias, sosteniendo además que no sólo las conjunciones, sino también las disyunciones tienen sentido sólo si corresponden a magnitudes compatibles. (Griffiths 1998, 1609; Griffiths y Omnès 1999, 28; Griffiths 2003, 1426). Otra postura sin embargo es la de la llamada lógica cuántica (Birkhoff y von Neumann 1936), que considera todas las operaciones bien definidas aun cuando las magnitudes asociadas sean incompatibles. En este caso, la expresión para estas operaciones en términos de proyectores, en particular para la intersección y la suma de subespacios, no es trivial (Mittelstaedt 1978, 20-21; Vanni 2010, 45).
. Si dos magnitudes son incompatibles, cumplen una relación de incerteza y, por consiguiente no es posible predicar sus propiedades de valor de modo simultáneo, es decir, como conjunciones (Ballentine 1990, 183; Sakurai 1994, 35). La postura tradicional consiste en sostener que las conjunciones tienen sentido sólo si corresponden a magnitudes compatibles. Esta es la postura adoptada en el formalismo de historias, sosteniendo además que no sólo las conjunciones, sino también las disyunciones tienen sentido sólo si corresponden a magnitudes compatibles. (Griffiths 1998, 1609; Griffiths y Omnès 1999, 28; Griffiths 2003, 1426). Otra postura sin embargo es la de la llamada lógica cuántica (Birkhoff y von Neumann 1936), que considera todas las operaciones bien definidas aun cuando las magnitudes asociadas sean incompatibles. En este caso, la expresión para estas operaciones en términos de proyectores, en particular para la intersección y la suma de subespacios, no es trivial (Mittelstaedt 1978, 20-21; Vanni 2010, 45).
Sin embargo, cuando se trata de la conjunción, disyunción, y negación de propiedades de valor de magnitudes compatibles, entonces las operaciones entre los correspondientes proyectores pueden definirse fácilmente. El operador de la conjunción es simplemente el producto de los operadores, es decir:
El operador de la disyunción, por otro lado, es la suma de los operadores menos el de la intercesión:
Y finalmente, el de la negación es:
Si ![]() y
y ![]() son además ortogonales, se tiene
son además ortogonales, se tiene ![]() , expresión ésta que justifica por qué la propiedad
, expresión ésta que justifica por qué la propiedad ![]() mencionada más arriba tiene el proyector indicado (Vanni 2010).
mencionada más arriba tiene el proyector indicado (Vanni 2010).
Dos nociones muy importantes en el formalismo de historias cuánticas son la noción de espacio muestral (Griffiths 1996, 2760; 1998, 1605) y, asociada a la anterior, la noción de contexto (Vanni, 2010, 48; Laura y Vanni 2010). Diremos que un particular espacio muestral asociado a una magnitud ![]() es el conjunto de propiedades que queda determinado por una partición completa en subconjuntos disjuntos de su espectro. En forma más clara, si
es el conjunto de propiedades que queda determinado por una partición completa en subconjuntos disjuntos de su espectro. En forma más clara, si ![]() es una magnitud representada por un operador en un espacio de Hilbert de dimensión
es una magnitud representada por un operador en un espacio de Hilbert de dimensión ![]() y su espectro viene dado por
y su espectro viene dado por ![]() , entonces una partición con el requerimiento mencionado será por ejemplo
, entonces una partición con el requerimiento mencionado será por ejemplo ![]() ,
, ![]() ,
, ![]() ,
, ![]() . De esta manera, el espacio muestral asociado a la magnitud
. De esta manera, el espacio muestral asociado a la magnitud ![]() , con esa partición, quedará determinado por el conjunto de propiedades representadas por los proyectores de la forma
, con esa partición, quedará determinado por el conjunto de propiedades representadas por los proyectores de la forma ![]() . La partición es disjunta porque cada
. La partición es disjunta porque cada ![]() tiene intersección nula con los restantes, y es completa porque la unión de todos los
tiene intersección nula con los restantes, y es completa porque la unión de todos los ![]() constituyen el espectro completo de
constituyen el espectro completo de ![]() . Esto resulta en el hecho de que los
. Esto resulta en el hecho de que los ![]() representen propiedades de valor, o rango de valores de
representen propiedades de valor, o rango de valores de ![]() , que son excluyentes y exhaustivas; por consiguiente, dichos
, que son excluyentes y exhaustivas; por consiguiente, dichos ![]() serán ortogonales,
serán ortogonales, ![]() , y además sumarán la identidad del espacio de Hilbert del sistema
, y además sumarán la identidad del espacio de Hilbert del sistema ![]() . Se dice que los
. Se dice que los ![]() que cumplen estas dos últimas propiedades forman una descomposición proyectiva de la identidad asociada a la magnitud
que cumplen estas dos últimas propiedades forman una descomposición proyectiva de la identidad asociada a la magnitud ![]() . Hacemos notar que los
. Hacemos notar que los ![]() no son necesariamente autoproyectores de, porque no necesariamente representan propiedades de valor único. Son suma de subconjuntos disjuntos de autoproyectores de
no son necesariamente autoproyectores de, porque no necesariamente representan propiedades de valor único. Son suma de subconjuntos disjuntos de autoproyectores de ![]() . Sólo en el caso particular de tener la partición más refinada posible del espectro de
. Sólo en el caso particular de tener la partición más refinada posible del espectro de ![]() , dada por
, dada por ![]() , tendremos que
, tendremos que ![]() . En ese caso, los
. En ese caso, los ![]() son iguales a los autoproyectores de
son iguales a los autoproyectores de ![]() , y así
, y así ![]() es la descomposición habitual de la identidad en términos de los autoproyectores de
es la descomposición habitual de la identidad en términos de los autoproyectores de ![]() . Otra cosa que es importante subrayar es que los proyectores que determinan una descomposición proyectiva conmutan entre sí; por lo tanto, representan propiedades cuánticas compatibles.
. Otra cosa que es importante subrayar es que los proyectores que determinan una descomposición proyectiva conmutan entre sí; por lo tanto, representan propiedades cuánticas compatibles.
Un contexto, por otro lado, es el conjunto de todas las propiedades formadas a partir de las disyunciones del espacio muestral, es decir a partir de las disyunciones de los elementos ![]() que forman una descomposición proyectiva de la identidad. Al ser los
que forman una descomposición proyectiva de la identidad. Al ser los ![]() ortogonales, las disyunciones que se generan a partir de éstos se reducen a simples sumas sobre los
ortogonales, las disyunciones que se generan a partir de éstos se reducen a simples sumas sobre los ![]() ; por lo tanto, cualquier propiedad del contexto se podrá representar como
; por lo tanto, cualquier propiedad del contexto se podrá representar como ![]() , con
, con ![]() igual o bien a 0, o bien a 1. Como vemos un contexto es generado completamente por un espacio muestral, y las propiedades asociadas a los
igual o bien a 0, o bien a 1. Como vemos un contexto es generado completamente por un espacio muestral, y las propiedades asociadas a los ![]() en el espacio muestral que generan dicho contexto, son llamadas elementos mínimos del contexto. De este modo, un contexto es el conjunto de todas las propiedades que se pueden predicar respecto de la magnitud
en el espacio muestral que generan dicho contexto, son llamadas elementos mínimos del contexto. De este modo, un contexto es el conjunto de todas las propiedades que se pueden predicar respecto de la magnitud ![]() y, por supuesto, de cualquier otra magnitud que conmuta con
y, por supuesto, de cualquier otra magnitud que conmuta con ![]() , ya que en ese caso tendrán un conjunto común de autoproyectores (Sakurai 1994, 29) y, por consiguiente podrán compartir un contexto común. Para cada magnitud
, ya que en ese caso tendrán un conjunto común de autoproyectores (Sakurai 1994, 29) y, por consiguiente podrán compartir un contexto común. Para cada magnitud ![]() , existirá un contexto que determina el universo de discurso de sus propiedades, las cuales son representadas por operadores que conmutan. Dos magnitudes incompatibles, es decir, cuyos operadores no conmutan, no podrán pertenecer a un contexto común.
, existirá un contexto que determina el universo de discurso de sus propiedades, las cuales son representadas por operadores que conmutan. Dos magnitudes incompatibles, es decir, cuyos operadores no conmutan, no podrán pertenecer a un contexto común.
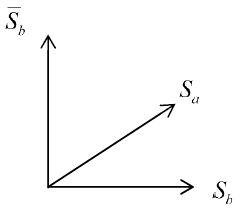
Es importante notar que, dentro de cada contexto, el conjunto de sus propiedades con las operaciones lógicas definidas arriba, forman una subestructura booleana (Vanni 2010, 48-49). Esto se debe esencialmente al hecho de que, en cada contexto, los proyectores que representan las propiedades dentro de él conmutan entre sí. Las características cuánticas asociadas a la pérdida de booleaneidad aparecen al combinar propiedades de distintos contextos. Esto puede verse en la representación dada por la Figura 1.
Tenemos las propiedades ![]() y su negación
y su negación ![]() correspondientes respectivamente a los subespacios
correspondientes respectivamente a los subespacios ![]() y
y ![]() , en la figura representados por los ejes cartesianos en un espacio de dimensión igual a 2. Consideremos que una propiedad
, en la figura representados por los ejes cartesianos en un espacio de dimensión igual a 2. Consideremos que una propiedad ![]() , representada por el subespacio
, representada por el subespacio ![]() , se asigna al sistema. Como vemos, el subespacio
, se asigna al sistema. Como vemos, el subespacio ![]() no está incluido en
no está incluido en ![]() , pero llamativamente, tampoco en su complemento
, pero llamativamente, tampoco en su complemento ![]() .
.
En términos de propiedades tenemos que dado ![]() , resulta
, resulta ![]() , ya que las rectas asociadas a
, ya que las rectas asociadas a ![]() y
y ![]() tienen al cero como intersección; pero por la misma razón, se tiene también que
tienen al cero como intersección; pero por la misma razón, se tiene también que ![]() . Esto es una característica que no tiene precedente clásico cuando pensamos a las propiedades en términos de conjuntos. Si un conjunto tiene intersección nula con otro, no puede tener también intersección nula con su complemento. Cuánticamente esta idea lógica elemental, propia de una estructura booleana, no se cumple.
. Esto es una característica que no tiene precedente clásico cuando pensamos a las propiedades en términos de conjuntos. Si un conjunto tiene intersección nula con otro, no puede tener también intersección nula con su complemento. Cuánticamente esta idea lógica elemental, propia de una estructura booleana, no se cumple.
Estas características cuánticas se han puesto de manifiesto en el ejemplo porque se ha predicado sobre propiedades pertenecientes a distintos contextos. Aquí ![]() es el espacio muestral que determina un contexto, donde valen las características booleanas, y
es el espacio muestral que determina un contexto, donde valen las características booleanas, y ![]() es el espacio muestral que determina otro contexto, donde también valen las características booleanas. Las características booleanas se pierden, sin embargo, cuando se intenta incorporar los dos contextos en otro que los contenga. Volveremos a encontrarnos con esta peculiaridad luego de definir una noción generalizada de contexto de historias.
es el espacio muestral que determina otro contexto, donde también valen las características booleanas. Las características booleanas se pierden, sin embargo, cuando se intenta incorporar los dos contextos en otro que los contenga. Volveremos a encontrarnos con esta peculiaridad luego de definir una noción generalizada de contexto de historias.
Hasta ahora hemos hablado de propiedades, pero además de ellas es necesario encontrar una representación de la noción de estado, por medio de la cual se asignan dichas propiedades al sistema. Pues bien, la forma más básica de representar el estado de un sistema cuántico es por medio de un vector de norma igual a uno en el espacio del Hilbert, que denotaremos con ![]() y llamamos vector de estado (Hughes 1989, 63; Sakurai 1994, 11). Una propiedad de valor correspondiente a una magnitud física, con certeza podrá asignarse a un sistema, si el vector de estado del sistema pertenece al subespacio asociado a la propiedad, y con certeza no podrá ser asignada si pertenece al complemento ortogonal de dicho subespacio. Como vemos, esto tiene una reminiscencia de la situación clásica en términos de pertenencia del estado clásico a una cierta región o a su complemento en el espacio de fase. Sin embargo, las diferencias son muchas, el estado puede no pertenecer ni al subespacio asociado a la propiedad, ni al complemento ortogonal de dicho subespacio; en este caso no puede afirmarse con certeza ni que la propiedad se asigna al sistema ni que la propiedad no se asigna.
y llamamos vector de estado (Hughes 1989, 63; Sakurai 1994, 11). Una propiedad de valor correspondiente a una magnitud física, con certeza podrá asignarse a un sistema, si el vector de estado del sistema pertenece al subespacio asociado a la propiedad, y con certeza no podrá ser asignada si pertenece al complemento ortogonal de dicho subespacio. Como vemos, esto tiene una reminiscencia de la situación clásica en términos de pertenencia del estado clásico a una cierta región o a su complemento en el espacio de fase. Sin embargo, las diferencias son muchas, el estado puede no pertenecer ni al subespacio asociado a la propiedad, ni al complemento ortogonal de dicho subespacio; en este caso no puede afirmarse con certeza ni que la propiedad se asigna al sistema ni que la propiedad no se asigna.
En el formalismo de operadores de estado, el vector de estado ![]() también puede ser representado por el correspondiente operador de estado
también puede ser representado por el correspondiente operador de estado ![]() que, como vemos, también es un proyector, y por lo tanto también representativo de una propiedad (Ballentine 1990, 37). Estados de este tipo, representados por un proyector, son llamados estados puros porque asignan certezas pero, a diferencia del caso clásico, no asignan certezas a todas las propiedades (Hughes 1989, 92); asignan certeza sólo un conjunto determinado de propiedades: el conjunto de propiedades representadas por el mismo proyector de estado
que, como vemos, también es un proyector, y por lo tanto también representativo de una propiedad (Ballentine 1990, 37). Estados de este tipo, representados por un proyector, son llamados estados puros porque asignan certezas pero, a diferencia del caso clásico, no asignan certezas a todas las propiedades (Hughes 1989, 92); asignan certeza sólo un conjunto determinado de propiedades: el conjunto de propiedades representadas por el mismo proyector de estado ![]() , con el agregado de todas aquéllas representadas por proyectores ortogonales a
, con el agregado de todas aquéllas representadas por proyectores ortogonales a ![]() .
.
En el caso más general, el estado de un sistema cuántico es representado por una mezcla de estados puros dada por ![]() , donde los
, donde los ![]() son reales positivos y suman uno (Ballentine 1990, 37; Sakurai 1994, 174-177). En este caso, el estado no puede asignar certeza a ninguna propiedad, sino sólo asigna probabilidades. La asignación de probabilidades está dada por la llamada regla de Born y vale para estados puros o no (Hughes 1989, 147; Ballentine 1990, 42). Si
son reales positivos y suman uno (Ballentine 1990, 37; Sakurai 1994, 174-177). En este caso, el estado no puede asignar certeza a ninguna propiedad, sino sólo asigna probabilidades. La asignación de probabilidades está dada por la llamada regla de Born y vale para estados puros o no (Hughes 1989, 147; Ballentine 1990, 42). Si ![]() es el operador de estado, y
es el operador de estado, y ![]() es el proyector asociado a una propiedad de valor
es el proyector asociado a una propiedad de valor ![]() , entonces dicha propiedad puede ser asignada al sistema con una probabilidad dada por
, entonces dicha propiedad puede ser asignada al sistema con una probabilidad dada por
donde el símbolo ![]() significa la traza del producto
significa la traza del producto ![]() (Hughes 1989, 136-137; Ballentine 1990, 7; Sakurai 1994, 38).
(Hughes 1989, 136-137; Ballentine 1990, 7; Sakurai 1994, 38).
La ecuación fundamental que rige la evolución temporal de un estado cuántico es la llamada ecuación de Schrödinger (Hughes 1989, 77-78; Ballentine 1990, 68; Sakurai 1994, 71-72). La información dinámica de esta evolución es a menudo representada en términos de la aplicación sobre el vector de estado del llamado operador de evolución, el cual, por su puesto, queda determinado por la ecuación Schrödinger. Llamaremos ![]() al operador de evolución del tiempo
al operador de evolución del tiempo ![]() al tiempo
al tiempo ![]() . Este operador cumple
. Este operador cumple ![]() ,
, ![]() , donde el símbolo
, donde el símbolo ![]() significa hermítico conjugado (Sakurai 1994, 15). El operador
significa hermítico conjugado (Sakurai 1994, 15). El operador ![]() es tal que, aplicado a un vector de estado al tiempo
es tal que, aplicado a un vector de estado al tiempo ![]() , nos devuelve el estado al tiempo
, nos devuelve el estado al tiempo ![]() , es decir
, es decir ![]() (Hughes 1989, 145-146; Ballentine 1990, 68-69; Sakurai 1994, 68-72).
(Hughes 1989, 145-146; Ballentine 1990, 68-69; Sakurai 1994, 68-72).
Al considerar que el estado evoluciona en el tiempo, las magnitudes físicas son consideradas fijas. Este es el llamado marco de Schrödinger. Los operadores que representan magnitudes físicas en el marco de Schrödinger son llamados operadores de Schrödinger (Ballentine 1990, 69). En el marco de Schrödinger los estados se indicaran con dependencia temporal, y las magnitudes físicas no. Sin embargo, haciendo uso del mismo operador de evolución, es posible considerar una descripción temporal físicamente equivalente donde el estado es asumido independiente del tiempo, y son las magnitudes físicas las que se consideran dependientes del tiempo. Este es el llamado marco de Heisenberg. Una magnitud física representada por un operador ![]() en el marco de Schrödinger se relaciona con la misma magnitud física
en el marco de Schrödinger se relaciona con la misma magnitud física ![]() en el marco de Heisenberg por medio de la formula
en el marco de Heisenberg por medio de la formula
donde ![]() es un tiempo de referencia usualmente tomado como cero (Ballentine 1990, 68-69; Sakurai 1994, 82).
es un tiempo de referencia usualmente tomado como cero (Ballentine 1990, 68-69; Sakurai 1994, 82).
Es importante enfatizar que un sistema cuántico evoluciona en el tiempo (de acuerdo con la ecuación de Schrödinger) de forma completamente determinista, de modo que conociendo el estado a un tiempo inicial ![]() , queda determinado con certeza el estado para todo tiempo posterior
, queda determinado con certeza el estado para todo tiempo posterior ![]() . Pese a ello, y aunque las magnitudes también puedan considerarse que evolucionan en el marco de Heisenberg en forma determinista, la evolución de los valores que dichas magnitudes pueden adoptar en términos de los resultados obtenidos en las mediciones es completamente indeterminista. Es en este punto que se recurre a una descripción probabilística, con la fórmula para las probabilidades dada por la regla de Born. (Hughes 1989, 78). Esta peculiar relación entre la evolución determinista del estado, y la asignación de propiedades en forma indeterminista producto de la medición, ha sido objeto de todo tipo de discusión y debate en el marco del llamado problema de la medición, del cual volveremos hablar más adelante.
. Pese a ello, y aunque las magnitudes también puedan considerarse que evolucionan en el marco de Heisenberg en forma determinista, la evolución de los valores que dichas magnitudes pueden adoptar en términos de los resultados obtenidos en las mediciones es completamente indeterminista. Es en este punto que se recurre a una descripción probabilística, con la fórmula para las probabilidades dada por la regla de Born. (Hughes 1989, 78). Esta peculiar relación entre la evolución determinista del estado, y la asignación de propiedades en forma indeterminista producto de la medición, ha sido objeto de todo tipo de discusión y debate en el marco del llamado problema de la medición, del cual volveremos hablar más adelante.
Con esta breve introducción de las principales características formales de la mecánica cuántica, en especial referida a su representación de propiedades, estamos en condiciones de abordar los distintos formalismos de historias cuánticas. Comenzaremos con el de Historias Consistentes, que puede considerarse como el formalismo fundacional de los demás formalismos de historias cuánticas.
2 Historias consistentes ↑
El formalismo de Historias Consistentes fue desarrollado inicialmente por Robert Griffiths en la década de los ‘80 (Griffiths 1884). Más tarde, de la mano de Roland Omnès, y posteriormente con los trabajos de Murray Gell-Mann y James Hartle, se desarrollaron ciertas variantes, aunque sin modificar la esencia de la propuesta (Omnès 1988; Gell-Mann y Hartle 1990).
La idea central del formalismo consiste en describir la evolución de un sistema cuántico en términos de historias construidas por medio de secuencia de propiedades consideradas a distintos tiempos. Bajo esta concepción, se prescinde de la noción de estado como el elemento que determina la evolución del sistema y que asigna propiedades de valor a las magnitudes. Ya sea el estado con su evolución, y las propiedades con su asignación, pasan a estar integradas en la misma noción de historia. Es cada historia, constituida de distintas propiedades a distintos tiempos, la que da cuenta de la evolución del sistema, la cual es considerada como una secuencia completamente estocástica desde su definición, y no debido a algún proceso de medición por medio del cual se introducen las probabilidades dadas por la regla de Born. El concepto de medición se despoja completamente de este papel especial de introducir el indeterminismo en la teoría (injustificado, por otro lado, puesto que los aparatos de medición están compuestos de los mismos sistemas microscópicos que la teórica cuántica pretende describir).
En el formalismo de historias consistentes, todas las dependencias temporales se consideran indeterministas. Esto no significa que la ecuación de Schrödinger deje de ser tenida en cuenta: simplemente es considerada para otro propósito. Por medio el operador de evolución, la ecuación de Schrödinger permitirá generar una noción de peso probabilístico a cada historia, lo cual tendrá una importancia fundamental. Sin embargo antes de presentar esta cuestión, será necesario establecer una estructura lógica de historias dentro de la cual cada historia es pensada como una proposición elemental de evolución del sistema. Empezaremos por la construcción basada en los trabajos de Griffiths.
2.1 La estructura lógica de historias de Griffiths ↑
Comencemos considerando un sistema cuántico en el marco de Schrödinger (donde las magnitudes físicas son consideradas fijas en el tiempo), con un espacio de Hilbert de dimensión ![]() , al que se quiere describir en términos de historias. Supongamos una secuencia de tiempos ordenada
, al que se quiere describir en términos de historias. Supongamos una secuencia de tiempos ordenada ![]() , y en cada tiempo
, y en cada tiempo ![]() consideramos una cierta magnitud física
consideramos una cierta magnitud física ![]() del sistema. En ese tiempo asumimos una particular descomposición proyectiva asociada
del sistema. En ese tiempo asumimos una particular descomposición proyectiva asociada ![]() , la cual suponemos representada por un conjunto de proyectores
, la cual suponemos representada por un conjunto de proyectores ![]() correspondiente al rango de valores
correspondiente al rango de valores ![]() del espectro de
del espectro de ![]() al tiempo
al tiempo ![]() . Por tratarse de una descomposición proyectiva, los
. Por tratarse de una descomposición proyectiva, los ![]() deberán cumplir (para cada
deberán cumplir (para cada ![]() )
) ![]() , y
, y ![]() , siendo
, siendo ![]() la identidad del espacio de Hilbert del sistema. El conjunto de proyectores
la identidad del espacio de Hilbert del sistema. El conjunto de proyectores ![]() representan las propiedades de rango de valor en
representan las propiedades de rango de valor en ![]() que conforman el espacio muestral asociado a la magnitud
que conforman el espacio muestral asociado a la magnitud ![]() en el tiempo
en el tiempo ![]() . De este modo, tendremos un espacio muestral de propiedades a cada tiempo.
. De este modo, tendremos un espacio muestral de propiedades a cada tiempo.
El siguiente paso es construir un espacio muestral de secuencias de propiedades tomadas del espacio muestral a cada tiempo, es decir, un espacio muestral de historias, que vistas como propiedades compuestas (de propiedades a distintos tiempos) puedan ser representadas por proyectores que constituyan una descomposición proyectiva de la identidad en un espacio de Hilbert de historias. La idea es que al definir operaciones lógicas dentro del espacio muestral de historias, dichas historias también puedan considerarse como proposiciones, proposiciones mínimas de evolución de cuyas disyunciones se pueda generar un contexto de historias, noción que, como hemos visto, nos asegura una estructura lógica booleana. El contexto de historias, con las magnitudes consideradas a los tiempos considerados, formará un universo de discurso de las evoluciones del sistema y respetará las leyes de la estructura lógica clásica.
Sin embargo, se presenta aquí la dificultad de cómo representar historias para construir su espacio muestral en términos de proyectores que constituyan una descomposición proyectiva, y así puedan generar el correspondiente contexto de historias. El problema consiste en incorporar la representación de las distintas propiedades que participan a distintos tiempos, aun cuando en general éstas pueden resultar incompatibles.
En el formalismo original de Griffiths, este problema se logra sortear considerando que la descripción de distintas propiedades de un mismo sistema a distintos tiempos es equivalente a la descripción de cada una de esas propiedades en un sistema dentro de una colección de sistemas considerados simultáneamente (Griffiths 1996, 2761; Griffiths 2002, 112). Dicho de otra manera, se asume que, para cada ![]() , el conjunto de los
, el conjunto de los ![]() constituye la descomposición proyectiva asociada a la variable
constituye la descomposición proyectiva asociada a la variable ![]() del sistema etiquetado con el índice
del sistema etiquetado con el índice ![]() dentro de un conjunto de
dentro de un conjunto de ![]() sistemas idénticos. De este modo, el proyector de una historia puede ser construido mediante el producto tensorial de los proyectores
sistemas idénticos. De este modo, el proyector de una historia puede ser construido mediante el producto tensorial de los proyectores ![]() . Así, una posible historia podrá representada por:
. Así, una posible historia podrá representada por:
donde ![]() indica el índice múltiple dado por
indica el índice múltiple dado por ![]() , siendo cada
, siendo cada ![]() el índice que etiqueta un proyector en descomposición proyectiva asociada a la variable al tiempo
el índice que etiqueta un proyector en descomposición proyectiva asociada a la variable al tiempo ![]() y que, por lo tanto, representa la propiedad de valor de
y que, por lo tanto, representa la propiedad de valor de ![]() en el rango
en el rango ![]() . El símbolo
. El símbolo ![]() representa el producto tensorial habitual (Hughes 1989, 148-149; Griffiths 2002, 82-85). Debido a que el espacio de Hilbert de una colección de sistemas es el producto tensorial de cada espacio de Hilbert por separado, tendremos que el espacio de Hilbert de historias, que llamaremos
representa el producto tensorial habitual (Hughes 1989, 148-149; Griffiths 2002, 82-85). Debido a que el espacio de Hilbert de una colección de sistemas es el producto tensorial de cada espacio de Hilbert por separado, tendremos que el espacio de Hilbert de historias, que llamaremos ![]() , será dado por
, será dado por ![]() , donde
, donde ![]() es copia de espacio de Hilbert
es copia de espacio de Hilbert ![]() usado para describir al sistema en cada tiempo. Con esta construcción es claro que los
usado para describir al sistema en cada tiempo. Con esta construcción es claro que los ![]() que representan las historias cumplen:
que representan las historias cumplen:
Siendo ![]() el operador identidad en el espacio de Hilbert
el operador identidad en el espacio de Hilbert ![]() . Es decir, los
. Es decir, los ![]() forman una descomposición proyectiva en el espacio de historias, y por consiguiente determinan un espacio muestral de historias.
forman una descomposición proyectiva en el espacio de historias, y por consiguiente determinan un espacio muestral de historias.
Contando con los proyectores del espacio muestral de historias, es posible definir la conjunción, la disyunción y la negación de historias en términos de operaciones entre sus correspondientes proyectores, en forma completamente análoga al modo en que hemos definido esas operaciones entre propiedades cuánticas ordinarias. Estos proyectores conmutan entre sí debido a que representan propiedades de un espacio muestral; por consiguiente, en analogía con las ecuaciones (1.2)-(1.4), el operador de la disyunción será ![]() , y finalmente, el de la negación
, y finalmente, el de la negación ![]() .
.
A partir de disyunciones entre los elementos del espacio muestral de historias, se podrá generar el correspondiente contexto de historias. Los ![]() , que representan el espacio muestral de historias, son los elementos mínimos del contexto y, como es propio de un contexto, cada historia en él podrá representada por sumas de dichos elementos. Más precisamente, un contexto de historias
, que representan el espacio muestral de historias, son los elementos mínimos del contexto y, como es propio de un contexto, cada historia en él podrá representada por sumas de dichos elementos. Más precisamente, un contexto de historias ![]() es el conjunto definido como:
es el conjunto definido como:
Un contexto de historias se dice también que forma una familia de historias (Griffith 1996, 2761; 2002, 116).
2.2 Ejemplo de construcción de una familia de historias ↑
Antes de seguir adelante, vale la pena fijar las ideas anteriores mediante un ejemplo de construcción de una familia de historias a dos tiempos. Supongamos un sistema con un espacio de Hilbert de dimensión ![]() , y los tiempos
, y los tiempos ![]() . Consideremos en
. Consideremos en ![]() la magnitud
la magnitud ![]() , cuyo espectro es
, cuyo espectro es ![]() , y que posee una descomposición proyectiva dada por
, y que posee una descomposición proyectiva dada por
El proyector ![]() corresponde al rango de valores de
corresponde al rango de valores de ![]() dado por
dado por ![]() , y
, y ![]() corresponde al rango de valores de
corresponde al rango de valores de ![]() dado por
dado por ![]() . Por otro lado, en el tiempo
. Por otro lado, en el tiempo ![]() consideramos la magnitud
consideramos la magnitud ![]() , cuyo espectro es
, cuyo espectro es ![]() , y que posee una descomposición proyectiva dada por
, y que posee una descomposición proyectiva dada por
En este caso, cada ![]() corresponde al rango de valores de
corresponde al rango de valores de ![]() dado por
dado por ![]() . Bajo estas condiciones, tendremos un espacio muestral de historias dado por el conjunto de los
. Bajo estas condiciones, tendremos un espacio muestral de historias dado por el conjunto de los ![]() , siendo aquí
, siendo aquí ![]() . Este conjunto estará formado por seis elementos, que serán los elementos mínimos del contexto. Explícitamente, tomando las dos posibilidades para el índice
. Este conjunto estará formado por seis elementos, que serán los elementos mínimos del contexto. Explícitamente, tomando las dos posibilidades para el índice ![]() correspondiente al primer tiempo, y las tres posibilidades para el índice
correspondiente al primer tiempo, y las tres posibilidades para el índice ![]() correspondiente al segundo tiempo, el espacio muestral resulta:
correspondiente al segundo tiempo, el espacio muestral resulta:
Desde el punto de vista lógico, este conjunto de seis historias, sujetas a las magnitudes consideradas y a los tiempos establecidos, constituyen las proposiciones básicas de evolución del sistema. Es decir, en términos de propiedades de las magnitudes consideradas, el sistema seguirá uno de esos seis caminos elementales, y aunque el formalismo no predice cuál, nos permite establecer, a partir de las disyunciones de estas seis historias elementales, un contexto de historias, o familia de historias ![]() , que constituye el universo de discurso que incluye todo lo que se puede predicar respecto de la evolución del sistema (sujeta a las magnitudes consideradas y a los tiempos establecidos). Se podrá, entonces, formular enunciados que aplican conectivos lógicos entre historias como parte de algún razonamiento, y aunque, como ya hemos mencionado, cuánticamente no contamos con una noción inferencia satisfactoria, podremos alcanzar conclusiones en términos de probabilidades que definiremos sobre las historias. Por ejemplo, en algún razonamiento podría incluirse el enunciado según el cual el sistema podrá seguir o bien la historia
, que constituye el universo de discurso que incluye todo lo que se puede predicar respecto de la evolución del sistema (sujeta a las magnitudes consideradas y a los tiempos establecidos). Se podrá, entonces, formular enunciados que aplican conectivos lógicos entre historias como parte de algún razonamiento, y aunque, como ya hemos mencionado, cuánticamente no contamos con una noción inferencia satisfactoria, podremos alcanzar conclusiones en términos de probabilidades que definiremos sobre las historias. Por ejemplo, en algún razonamiento podría incluirse el enunciado según el cual el sistema podrá seguir o bien la historia ![]() o bien la historia
o bien la historia ![]() ; esto significa que es necesario formular la disyunción
; esto significa que es necesario formular la disyunción ![]() , lo cual resulta en un elemento del contexto dado por:
, lo cual resulta en un elemento del contexto dado por:
Este ejemplo muestra cómo construir el contexto de historias y operar entre ellas. Sin embargo, como ya hemos mencionado, en este formalismo se considera la mecánica cuántica como una teoría completamente estocástica. Por lo tanto, aún debe definirse una medida de probabilidad sobre el universo de historias, necesaria para hacer predicciones en términos de razonamientos probabilísticos, y en particular, inferencias de certeza, que corresponderán a probabilidades iguales a 1 o a 0.
2.3 Peso probabilístico sobre historias ↑
Siguiendo los trabajos originales de Griffith (Griffith 1996, 2761; 2002, 137), antes de definir una medida de probabilidad se define el llamado operador cadena, que incorpora en cada historia la información dinámica contenida en la ecuación de Schrödinger por medio de los operadores de evolución ![]() . Si
. Si ![]() es el proyector de una historia en el espacio de Hilbert
es el proyector de una historia en el espacio de Hilbert ![]() , entonces, el operador cadena
, entonces, el operador cadena ![]() es el resultado de la aplicación
es el resultado de la aplicación ![]() sobre el proyector de la historia, aplicación definida como
sobre el proyector de la historia, aplicación definida como
donde ![]() es un tiempo de referencia independiente de los otros tiempos que aparecen en la expresión, y que puede ser tomado igual a
es un tiempo de referencia independiente de los otros tiempos que aparecen en la expresión, y que puede ser tomado igual a ![]() . Como vemos, la aplicación
. Como vemos, la aplicación ![]() es un mapeo lineal de operadores en el espacio de Hilbert de historias
es un mapeo lineal de operadores en el espacio de Hilbert de historias ![]() a operadores en el espacio Hilbert
a operadores en el espacio Hilbert ![]() del sistema. Matemáticamente,
del sistema. Matemáticamente, ![]() (Griffiths 1996, 2761; 2002, 138). En el ejemplo anterior, tomando
(Griffiths 1996, 2761; 2002, 138). En el ejemplo anterior, tomando ![]() y
y ![]() tenemos que
tenemos que
La aplicación ![]() toma un proyector suma de proyectores de historias, y nos devuelve el operador cadena
toma un proyector suma de proyectores de historias, y nos devuelve el operador cadena ![]() correspondiente, que es la suma de operadores cadena por separado. Es fácil demostrar, haciendo uso de las propiedades de los operadores de evolución, que
correspondiente, que es la suma de operadores cadena por separado. Es fácil demostrar, haciendo uso de las propiedades de los operadores de evolución, que ![]() se puede expresar como
se puede expresar como
Donde los ![]() , de acuerdo con la ecuación (1.6), son los proyectores de Heisenberg correspondientes a los proyectores de Schrödinger
, de acuerdo con la ecuación (1.6), son los proyectores de Heisenberg correspondientes a los proyectores de Schrödinger ![]() (es decir, fijos en el tiempo), pero que determinan la descomposición espectral al tiempo
(es decir, fijos en el tiempo), pero que determinan la descomposición espectral al tiempo ![]() .
.
Con el operador cadena se define el peso probabilístico ![]() de la historia
de la historia ![]() (Griffiths 1996, 2762; 2002, 139) de la siguiente manera:
(Griffiths 1996, 2762; 2002, 139) de la siguiente manera:
El peso así definido responde a las propiedades de un producto interno y, en consecuencia, es un número real no negativo, y es cero si y sólo si el operador ![]() es cero (Griffiths 1996, 2762; 2002, 139).
es cero (Griffiths 1996, 2762; 2002, 139).
Si consideramos en el tiempo ![]() un proyector inicial fijo
un proyector inicial fijo ![]() , que puede considerarse como el estado (en este caso puro) del sistema en ese tiempo inicial, la familia de historias se podrá escribir
, que puede considerarse como el estado (en este caso puro) del sistema en ese tiempo inicial, la familia de historias se podrá escribir ![]() ; entonces, el peso
; entonces, el peso ![]() sobre esa historia adopta la forma
sobre esa historia adopta la forma
Si consideramos ahora el operador ![]() , con
, con ![]() , esto es, el operador que representa la historia
, esto es, el operador que representa la historia ![]() pero desde el tiempo
pero desde el tiempo ![]() al tiempo
al tiempo ![]() , el peso probabilístico sobre se puede escribir como:
, el peso probabilístico sobre se puede escribir como:
Ésta es la fórmula para el peso probabilístico de una historia que define Roland Omnès en su formulación de historias consistentes, y la misma puede generalizarse para estados iniciales ![]() no necesariamente puros (Omnès 1988, 904; 1992, 344; 1994, 129; 1999, 144-146). El operador
no necesariamente puros (Omnès 1988, 904; 1992, 344; 1994, 129; 1999, 144-146). El operador ![]() , que llamaremos operador de Omnès de la historia
, que llamaremos operador de Omnès de la historia ![]() , no es más que el hermítico conjugado del operador cadena
, no es más que el hermítico conjugado del operador cadena ![]() , pero sin considerar el tiempo
, pero sin considerar el tiempo ![]() . La ecuación (2.6) formulada por Griffiths es completamente equivalente a la ecuación (2.7) formulada por Omnès. Esta última quizás es más conveniente para justificar la definición del peso sobre las historias, pues si la historia se compone de propiedades de magnitudes todas compatibles entre sí, entonces el operador de Omnès
. La ecuación (2.6) formulada por Griffiths es completamente equivalente a la ecuación (2.7) formulada por Omnès. Esta última quizás es más conveniente para justificar la definición del peso sobre las historias, pues si la historia se compone de propiedades de magnitudes todas compatibles entre sí, entonces el operador de Omnès ![]() es el proyector correspondiente a la conjunción de las propiedades en la historias, y la ecuación (2.7) se reduce a la regla de Born usual aplicada al proyector de esa conjunción (Omnès 1999, 146).
es el proyector correspondiente a la conjunción de las propiedades en la historias, y la ecuación (2.7) se reduce a la regla de Born usual aplicada al proyector de esa conjunción (Omnès 1999, 146).
2.4 La estructura lógica de historias de Omnès ↑
Trabajar con las historias directamente en términos de los ![]() tiene a veces algunas ventajas a la hora de calcular sus probabilidades. Sin embargo, la desventaja es que los
tiene a veces algunas ventajas a la hora de calcular sus probabilidades. Sin embargo, la desventaja es que los ![]() no pueden servir como elementos para elaborar un contexto dentro del cual poder operar con conectivos lógicos de modo tal de generar una estructura booleana. Esto es así porque, tal como fueron definidos, en general los
no pueden servir como elementos para elaborar un contexto dentro del cual poder operar con conectivos lógicos de modo tal de generar una estructura booleana. Esto es así porque, tal como fueron definidos, en general los ![]() ni siquiera son proyectores. Son simplemente secuencias de multiplicaciones ordenadas de los proyectores de Heisenberg que intervienen en la historias, y éstos pueden no conmutar. Los
ni siquiera son proyectores. Son simplemente secuencias de multiplicaciones ordenadas de los proyectores de Heisenberg que intervienen en la historias, y éstos pueden no conmutar. Los ![]() son útiles para calcular probabilidades, pero con ellos perdemos la estructura lógica para formular enunciados que involucren operaciones entre historias.
son útiles para calcular probabilidades, pero con ellos perdemos la estructura lógica para formular enunciados que involucren operaciones entre historias.
Para sortear este inconveniente, Omnès define un “espacio geométrico de historias” (Omnès 1992, 345; 1994, 156-157; 1999, 141; Vanni 2010, 79). En este espacio, de dimensión igual a la cantidad de tiempos en las historias, cada eje se asocia a un tiempo ![]() . En cada uno de esos eje se representa el espectro de la magnitud
. En cada uno de esos eje se representa el espectro de la magnitud ![]() considerada en ese tiempo, y el eje se divide en intervalos
considerada en ese tiempo, y el eje se divide en intervalos ![]() , correspondientes a la división del espectro de
, correspondientes a la división del espectro de ![]() que determina su espacio muestral asociado a ese tiempo. Con esta construcción geométrica, cada historia dada por el operador
que determina su espacio muestral asociado a ese tiempo. Con esta construcción geométrica, cada historia dada por el operador ![]() queda representada por un bloque elemental
queda representada por un bloque elemental ![]() de dimensión
de dimensión ![]() , formado por el producto directo de los intervalos
, formado por el producto directo de los intervalos ![]() , es decir
, es decir ![]() , con
, con ![]() . Dicha construcción permite definir la estructura lógica de historias en términos de operaciones entre los bloques
. Dicha construcción permite definir la estructura lógica de historias en términos de operaciones entre los bloques ![]() , asociando los conectivos lógicos de conjunción, disyunción y negación a las operaciones habituales de intersección, unión y complemento, respectivamente, entre conjuntos de bloques
, asociando los conectivos lógicos de conjunción, disyunción y negación a las operaciones habituales de intersección, unión y complemento, respectivamente, entre conjuntos de bloques ![]() en el espacio geométrico de historias.
en el espacio geométrico de historias.
La estructura lógica así definida, en términos de operaciones entre bloques ![]() en el espacio geométrico de historias de Omnès, resulta booleana, la cual es completamente equivalente a la que resulta de las operaciones entre los operadores de historias
en el espacio geométrico de historias de Omnès, resulta booleana, la cual es completamente equivalente a la que resulta de las operaciones entre los operadores de historias ![]() definidos por Griffiths. Cada bloque
definidos por Griffiths. Cada bloque ![]() en el espacio geométrico de historias representa al operador de Omnès
en el espacio geométrico de historias representa al operador de Omnès ![]() , y éste se corresponde a su vez con el operador de Griffiths
, y éste se corresponde a su vez con el operador de Griffiths ![]() .
.
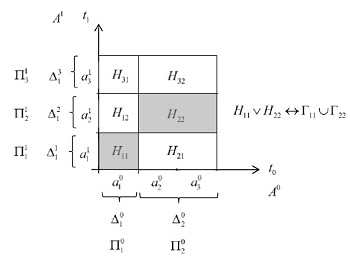
Un caso particular de esta construcción puede verse en la Figura 2, donde hemos representado el espacio geométrico de historias para el ejemplo de historias de Griffiths a dos tiempos presentado en la subsección 2.2. Aquí, para considerar estas historias como historias de Omnès, simplemente suponemos que las historias comienzan en ![]() , y que el tiempo de preparación del estado es algún otro tiempo anterior a
, y que el tiempo de preparación del estado es algún otro tiempo anterior a ![]() . En la figura se representa en sombreado la disyunción de las historias
. En la figura se representa en sombreado la disyunción de las historias ![]() y
y ![]() . Esta disyunción corresponde a la región dada por la unión de bloques
. Esta disyunción corresponde a la región dada por la unión de bloques ![]() , y que, en términos de operaciones entre los operadores de Griffiths, se expresa como
, y que, en términos de operaciones entre los operadores de Griffiths, se expresa como ![]() , y cuyo operador cadena además adquiere la forma
, y cuyo operador cadena además adquiere la forma ![]() en el marco de Heisenberg.
en el marco de Heisenberg.
En sus trabajos, Omnès completa la estructura lógica construida a partir del espacio geométrico de historias, definiendo una noción de inferencia lógica en términos probabilísticos. Para ello, en primer lugar define el peso probabilístico condicional. Supongamos dos historias ![]() y
y ![]() , representadas en términos de los operadores de Omnès. El peso condicional se define como ha de esperarse de la fórmula de una probabilidad condicional:
, representadas en términos de los operadores de Omnès. El peso condicional se define como ha de esperarse de la fórmula de una probabilidad condicional:
La inferencia es definida de modo tal que, si ![]() , entonces (Omnès 1992, 347; 1994, 157; 1988, 142)
, entonces (Omnès 1992, 347; 1994, 157; 1988, 142)
Esta noción de inferencia será de gran utilidad en muchos razonamientos formulados en el ámbito del formalismo de historias consistentes. Después de todo, al considerar la mecánica cuántica una teoría completamente estocástica, es natural pensar que las consecuencias físicas de la teoría se expresen en términos de probabilidades condicionales.
2.5 Condiciones de consistencia ↑
Hasta aquí hemos hablamos de peso probabilístico sobre historias, y no directamente de probabilidad sobre historias. La razón es que, si bien ![]() cumple algunos requisitos mínimos para considerarse una probabilidad, en rigor no los cumple todos, al menos no en todas las posibles familias de historias tal como han sido definidas. Lo que sucede es que, en general,
cumple algunos requisitos mínimos para considerarse una probabilidad, en rigor no los cumple todos, al menos no en todas las posibles familias de historias tal como han sido definidas. Lo que sucede es que, en general, ![]() no satisface los axiomas de Kolmogorov para una medida de probabilidad clásica (Mittelstaedt 1998, 74). Lo que falla es que
no satisface los axiomas de Kolmogorov para una medida de probabilidad clásica (Mittelstaedt 1998, 74). Lo que falla es que ![]() no es aditivo para historias disjuntas (Omnès 1999, 157-160; Griffiths 1984, 224). En términos de los operadores Griffiths esto significa que, si
no es aditivo para historias disjuntas (Omnès 1999, 157-160; Griffiths 1984, 224). En términos de los operadores Griffiths esto significa que, si ![]() , en general no se cumple que
, en general no se cumple que ![]() , como se esperaría de una probabilidad bien definida. La única excepción es para historias a dos tiempos; se puede probar que todo conjunto de historias a dos tiempos es consistente, pero un conjunto genérico no lo es (Vanni 2010, 81).
, como se esperaría de una probabilidad bien definida. La única excepción es para historias a dos tiempos; se puede probar que todo conjunto de historias a dos tiempos es consistente, pero un conjunto genérico no lo es (Vanni 2010, 81).
Al efectuar los cálculos explícitos de ![]() para historias
para historias ![]() y
y ![]() cualesquiera dentro de una familia, resulta que siempre aparecen la suma
cualesquiera dentro de una familia, resulta que siempre aparecen la suma ![]() más términos adicionales. Aunque los cálculos generales son algo engorrosos, resultan muy fáciles para historias a tres tiempos (Vanni 2010, 83-84). La idea es buscar familias donde los términos adicionales se anulen, y así
más términos adicionales. Aunque los cálculos generales son algo engorrosos, resultan muy fáciles para historias a tres tiempos (Vanni 2010, 83-84). La idea es buscar familias donde los términos adicionales se anulen, y así ![]() pueda considerarse una medida de probabilidad clásica. Esta exigencia se traduce en las llamadas condiciones de consistencia. Se puede demostrar que
pueda considerarse una medida de probabilidad clásica. Esta exigencia se traduce en las llamadas condiciones de consistencia. Se puede demostrar que ![]() cumple aditividad dentro de una familia de historias si, para cualquier par de historias disjuntas
cumple aditividad dentro de una familia de historias si, para cualquier par de historias disjuntas ![]() y
y ![]() en dicha familia, se cumple que
en dicha familia, se cumple que
Cuando una familia de historias, como las que hemos construido, cumple además esta última condición, se dice que es una familia de historias consistentes. En ese caso, la familia no sólo forma un contexto de historias cuya estructura lógica es booleana, sino que además está definida una probabilidad que respeta los axiomas de Kolmogorov para una medida de probabilidad clásica. Una familia de historias consistentes se llama también “framework” (Griffiths 1996, 2761; 2002, 141).
La ecuación (2.9) es condición necesaria y suficiente para que el peso probabilístico ![]() cumpla aditividad dentro de una familia. A veces es llamada condición de consistencia de Griffiths (Vanni 2010, 85), o condición de consistencia débil (Griffiths 1996, 2762). Por razones técnicas, a veces es conveniente exigir como condición de consistencia no sólo que la parte real de la expresión en (2.9) se anule, sino que también lo haga la parte imaginaria, con lo cual la condición se convierte en
cumpla aditividad dentro de una familia. A veces es llamada condición de consistencia de Griffiths (Vanni 2010, 85), o condición de consistencia débil (Griffiths 1996, 2762). Por razones técnicas, a veces es conveniente exigir como condición de consistencia no sólo que la parte real de la expresión en (2.9) se anule, sino que también lo haga la parte imaginaria, con lo cual la condición se convierte en
Esta última ecuación (2.10) es condición suficiente, pero no necesaria para que ![]() cumpla aditividad dentro de una familia. A veces es llamada condición de consistencia de Gell-Mann y Hartle, ya que fueron quienes la consideraron por primera vez (Gell-Mann y Hartle 1990, 327; 1993, 3353). A veces también es llamada condición de consistencia fuerte (Griffiths 1996, 2762).
cumpla aditividad dentro de una familia. A veces es llamada condición de consistencia de Gell-Mann y Hartle, ya que fueron quienes la consideraron por primera vez (Gell-Mann y Hartle 1990, 327; 1993, 3353). A veces también es llamada condición de consistencia fuerte (Griffiths 1996, 2762).
En la formalización de Omnès, si ![]() y
y ![]() representan dos historias disjuntas, la condición de consistencia débil adopta la forma
representan dos historias disjuntas, la condición de consistencia débil adopta la forma
Y de forma análoga, la condición de consistencia fuerte resulta
Como vemos, las condiciones de consistencia, tal como son presentadas por Omnès, quedan en dependencia explicita del estado inicial ![]() con el que se prepara al sistema. Esto puede cuestionarse, pues las condiciones que determinan un espacio muestral válido en términos probabilísticos en general quedan definidas previamente a cualquier noción de estado sobre el sistema (Griffiths 1996, 2774; Vanni 2010, 87). Como en las condiciones formuladas por Griffiths no se considera el operador al tiempo inicial como representante de un estado del sistema, éstas parecen más independientes respecto del estado inicial.
con el que se prepara al sistema. Esto puede cuestionarse, pues las condiciones que determinan un espacio muestral válido en términos probabilísticos en general quedan definidas previamente a cualquier noción de estado sobre el sistema (Griffiths 1996, 2774; Vanni 2010, 87). Como en las condiciones formuladas por Griffiths no se considera el operador al tiempo inicial como representante de un estado del sistema, éstas parecen más independientes respecto del estado inicial.
Vale la pena enfatizar que, para que una familia ![]() sea considerada consistente, las condiciones de consistencia se deben cumplir para todo par de historias disjuntas de la familia. Sin embargo, debido a la linealidad del operador cadena y la traza definida entre operadores, es suficiente que las condiciones de consistencia se cumplan para cualquier par de elementos mínimos
sea considerada consistente, las condiciones de consistencia se deben cumplir para todo par de historias disjuntas de la familia. Sin embargo, debido a la linealidad del operador cadena y la traza definida entre operadores, es suficiente que las condiciones de consistencia se cumplan para cualquier par de elementos mínimos ![]() distintos que genera la familia, para que toda la familia
distintos que genera la familia, para que toda la familia ![]() sea consistente.
sea consistente.
2.6 Refinamiento y compatibilidad ↑
Una familia de historias consistentes determina un marco descriptivo de evoluciones de un sistema en términos de propiedades de valor de ciertas magnitudes consideradas. Una vez establecido ese marco, podría desearse refinarlo al incorporar más propiedades que las consideradas en las descripciones. Esto puede lograrse o bien mediante un refinamiento temporal, es decir, agregando más tiempos en las historias con nuevas propiedades a considerar a esos tiempos, o bien con un refinamiento de propiedades a un dado tiempo, es decir, agregando más propiedades al espacio muestral en un tiempo ya dado en la historia.
El refinamiento de una familia de historias o contexto de historias queda determinado por el refinamiento del espacio muestral que lo genera. En términos de los operadores de Griffiths ![]() , cualquiera de los dos casos recién mencionados se logra al reemplazar uno o más proyectores en
, cualquiera de los dos casos recién mencionados se logra al reemplazar uno o más proyectores en ![]() por otros proyectores que, sumados, sean equivalentes a los que se reemplaza. Esta operación incluye el refinamiento temporal, pues cada tiempo adicional que no aparece en
por otros proyectores que, sumados, sean equivalentes a los que se reemplaza. Esta operación incluye el refinamiento temporal, pues cada tiempo adicional que no aparece en ![]() puede pensarse representado por el proyector identidad. Por ejemplo, supongamos que tenemos una familia a dos tiempos
puede pensarse representado por el proyector identidad. Por ejemplo, supongamos que tenemos una familia a dos tiempos ![]() y
y ![]() determinada por el espacio muestral de historias representadas por el conjunto de los
determinada por el espacio muestral de historias representadas por el conjunto de los ![]() , aquí
, aquí ![]() . Para hacer un refinamiento temporal, por ejemplo agregando un tiempo intermedio
. Para hacer un refinamiento temporal, por ejemplo agregando un tiempo intermedio ![]() entre
entre ![]() y
y ![]() , consideramos que
, consideramos que ![]() . Así, el refinamiento temporal se logra al efectuar el reemplazo:
. Así, el refinamiento temporal se logra al efectuar el reemplazo:
Por otro lado, un refinamiento de propiedades en un dado tiempo, por ejemplo en el tiempo ![]() , se logra al efectuar el reemplazo:
, se logra al efectuar el reemplazo:
Se dice que dos familias de historias consistentes tienen un refinamiento común si existe una tercera familia que las contenga y sea consistente. El refinamiento común más “grueso” entre dos familias, ![]() con elementos mínimos
con elementos mínimos ![]() , y
, y ![]() con elementos mínimos
con elementos mínimos ![]() , es la familia consistente generada por el conjunto de elementos mínimos formados por
, es la familia consistente generada por el conjunto de elementos mínimos formados por ![]() . Por ejemplo, dadas la familia
. Por ejemplo, dadas la familia ![]() generada por el conjunto de elementos mínimos
generada por el conjunto de elementos mínimos ![]() , y la familia
, y la familia ![]() generada por el conjunto de elementos mínimos
generada por el conjunto de elementos mínimos ![]() , entonces el refinamiento común más “grueso” es la familia consistente generada por el conjunto de elementos mínimos constituido por
, entonces el refinamiento común más “grueso” es la familia consistente generada por el conjunto de elementos mínimos constituido por ![]() . Por supuesto, un refinamiento común entre dos familias será imposible si algún elemento mínimo en una no conmuta con algún elemento mínimo en otra, porque en ese caso ni siquiera se podrá formar un contexto que determine un algebra booleana. Esto nos conduce a la noción de compatibilidad e incompatibilidad entre familias.
. Por supuesto, un refinamiento común entre dos familias será imposible si algún elemento mínimo en una no conmuta con algún elemento mínimo en otra, porque en ese caso ni siquiera se podrá formar un contexto que determine un algebra booleana. Esto nos conduce a la noción de compatibilidad e incompatibilidad entre familias.
Decimos que dos familias son compatibles si existe un refinamiento común entre ellas, y decimos que son incompatibles si esto no sucede. Esto implica dos nociones distintas de incompatibilidad entre familias. La primera es la noción habitual de incompatibilidad cuántica, que proviene de considerar propiedades cuyos operadores no conmutan. Si dos operadores de historia no conmutan, no pueden pertenecer a un mismo contexto o familia de historias y, por lo tanto no formarán parte de una estructura lógica clásica. Sin embargo, en el formalismo de historias consistentes, la incompatibilidad puede provenir de una fuente distinta a la falta de conmutatividad. Es posible tener dos familias, cada una consistente por separado, y donde cada uno de los operadores de historia de una familia conmuta con cada uno de los operadores de historia de la otra, pero aun así resultar que no puedan integrarse en una familia más grande que sea consistente. En ese caso la incompatibilidad proviene de la imposibilidad de cumplir las condiciones de consistencia que aseguran una medida de probabilidad válida; por consiguiente, no se puede asegurar la consistencia de razonamientos probabilísticos (en términos de probabilidades condicionales, por ejemplo) que mezclen historias de las distintas familias. En definitiva, la noción de compatibilidad en historias consistentes implica dos aspectos: primero, poder operar con enunciados que formen parte de una estructura booleanas; segundo, poder formular con tales enunciados razonamientos probabilísticos válidos.
Un ejemplo muy instructivo, en el cual existe incompatibilidad debido a la falta de un refinamiento común, es la llamada paradoja de las tres cajas (Griffiths 1996, 2770; 1998, 1616; 2002, 304). Esta paradoja fue inicialmente enunciada por Yakir Aharonov y Lev Vaidman (Aharonov y Vaidman, 1991). Supongamos una partícula que puede estar ubicada en tres cajas ![]() ,
, ![]() o
o ![]() . Cada caja puede concebirse como un estado para la partícula,
. Cada caja puede concebirse como un estado para la partícula, ![]() ,
, ![]() o
o ![]() . Estos estados deberán ser ortogonales porque son excluyentes, es decir, la presencia en una caja implica ausencia en las otras. Así el sistema puede describirse con un espacio de Hilbert de dimensión tres, donde
. Estos estados deberán ser ortogonales porque son excluyentes, es decir, la presencia en una caja implica ausencia en las otras. Así el sistema puede describirse con un espacio de Hilbert de dimensión tres, donde ![]() ,
, ![]() ,
, ![]() forman una base. Cada uno de estos estados, por ser estados puros, quedan asociados a las propiedades correspondientes representadas por
forman una base. Cada uno de estos estados, por ser estados puros, quedan asociados a las propiedades correspondientes representadas por ![]() ,
, ![]() ,
, ![]() , donde
, donde ![]() es la identidad del espacio de Hilbert de la partícula. Supongamos un estado inicial para la partícula en el tiempo
es la identidad del espacio de Hilbert de la partícula. Supongamos un estado inicial para la partícula en el tiempo ![]() dado por
dado por ![]() , asociado a la propiedad representada por
, asociado a la propiedad representada por ![]() , y un estado final al tiempo
, y un estado final al tiempo ![]() dado por
dado por ![]() , asociado a la propiedad representada por
, asociado a la propiedad representada por ![]() . Consideremos ahora dos familias de historias a tres tiempos, con un tiempo intermedio
. Consideremos ahora dos familias de historias a tres tiempos, con un tiempo intermedio ![]() .
.
Primero consideremos la familia de historias ![]() generada por el espacio muestral que determina la descomposición de la identidad
generada por el espacio muestral que determina la descomposición de la identidad ![]() en el espacio de historias de la siguiente manera:
en el espacio de historias de la siguiente manera: