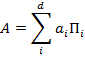Historias en mecánica cuántica

La premisa básica del formalismo de historias cuánticas consiste en abandonar la descripción de los sistemas cuánticos en términos de la evolución del estado, regida por la ecuación de Schrödinger. Las evoluciones pasan a ser descriptas en términos de historias, las cuales son entendidas como secuencias estocásticas de propiedades a distintos tiempos. El logro del formalismo es que permite lidiar con las dificultades conceptuales que resultan de la estructura lógica de las propiedades cuánticas, que no respeta la estructura lógica clásica, y a la vez permite desprenderse de la peculiar relación que la interpretación ortodoxa establece entre la evolución del estado cuántico y la asignación de propiedades al sistema en consideración. Si bien el formalismo de historias no puede predecir qué historia se actualizará en el decurso de los eventos, puede determinar condiciones específicas que establecen el conjunto de historias posibles para las propiedades y tiempos considerados. Este conjunto es una suerte de “mapa" de las posibles evoluciones que puede desarrollar el sistema. Dichas evoluciones serán aquéllas que, con una fórmula de la probabilidad previamente definida, cumplan los axiomas de la probabilidad clásica. En términos lógicos, el conjunto de todas las historias posibles determina el universo de discurso del sistema, siendo cada historia considerada como una “proposición elemental de evolución”, es decir, la entidad mínima por medio de la cual es posible describir la dinámica del sistema.

En la presente entrada, en primer lugar presentaremos las bases mínimas necesarias para comprender los aspectos fundamentales de la estructura lógica de las propiedades cuánticas, y luego desarrollaremos dos versiones del formalismo de historias cuánticas: el de Historias Consistentes y el de Historias Contextuales.

Estructura de propiedades cuánticas   ↑

La utilidad de cualquier teoría física consiste en su capacidad de describir las propiedades de los sistemas que estudia, operando con ellas en algún tipo de estructura lógica. Sólo así se podrá entender, explicar y predecir el comportamiento de esos sistemas. Para lograr esto, la teoría debe ser capaz de incorporar elementos formales capaces de representar dichas propiedades en un marco teórico específico.

Cuando hablamos de propiedades de un sistema, aquí nos estamos refiriendo a propiedades de valor que toman sus magnitudes. Por ejemplo, una magnitud fundamental de cualquier sistema físico es su energía . Asignar una determinada “propiedad de valor” a la magnitud energía es asignar o establecer un valor, o rango de valores a su energía. Así, “energía igual a 5 ergios”, “energía entre 5 y 7 ergios”, son ejemplos de propiedades de valor un sistema físico.

La mecánica clásica y la mecánica cuántica poseen diferentes elementos formales, sujetos a diferentes estructuras algebraicas, para representar sus propiedades. Estas diferencias son la base sobre la cual radica gran parte de las dificultades conceptuales encontradas a la hora de compatibilizar ambas teorías. En la física clásica, las propiedades de valor de un sistema pueden representarse por subconjuntos o regiones en el llamado espacio de fases del sistema (Hughes 1989, 58). El estado, por otro lado, se representa con un punto en ese espacio. Una propiedad se verifica en el sistema si el estado, como punto, pertenece a la región que representa la propiedad. Esto determina una particular estructura de propiedades en términos de operaciones entre conjuntos.

En términos lógicos, cada propiedad, o más exactamente, cada clase de propiedades lógicamente equivalentes, se puede identificar con una proposición, la proposición que adjudica la propiedad al sistema (Hughes 1989, 182). Con esta identificación, podemos transformar la estructura de propiedades en una estructura lógica. En el caso clásico esto se logra definiendo los conectivos lógicos de conjunción , disyunción , y negación  en términos de operaciones de intersección, unión y complemento entre conjuntos respectivamente (Hughes 1989, 181-182; Omnès 1999, 101; Vanni 2010, 36). La estructura lógica de propiedades así establecida responde a un algebra booleana, la cual es en esencia el álgebra que establece las operaciones entre conjuntos (Hughes 1989, 178-184; Bub 1997, 15-22; Boole 2009). En este tipo de estructura es posible además establecer una relación de implicación, de suma importancia para los razonamientos lógicos, que es compatible con la relación de inclusión entre conjuntos y permite una asignación de verdad consistente sobre la estructura lógica (Hughes 1989, 202; Omnès 1992, 347; Omnès 1994, 184-185; Bub 1997, 15-20). Sin embargo, esto último y muchas de las características booleanas de la estructura lógica clásica dejan de ser válidas en la mecánica cuántica. Para comprender este punto, es necesario explicar cómo se describen cuánticamente las magnitudes físicas y sus propiedades de valor.

En la mecánica cuántica, las magnitudes físicas se representan mediante operadores hermíticos que actúan sobre vectores en el llamado espacio de Hilbert  del sistema (Hughes 1989, 63-65; Ballentine 1990, 2-8; Sakurai 1994, 14-16). Aclaramos aquí que, aunque la magnitud no es el objeto que la representa en la teoría, en este caso un operador, en lo que sigue la identificaremos con el operador. Así diremos “magnitud ” y escribiremos el operador correspondiente.

Cada espacio de Hilbert  tiene subespacios, que son subconjuntos de  que contienen el vector nulo, y además son cerrados ante sumas y multiplicaciones por un escalar (Hughes 1989, 35). Podemos decir que, en mecánica cuántica, las magnitudes físicas toman valores sobre ciertos subespacios en el espacio de Hilbert del sistema. Esto se puede ver al considerar que, debido a la llamada descomposición espectral (Hughes 1989, 50; Ballentine 1990, 10-11), cualquier operador hermítico en un espacio de Hilbert de dimensión igual a  (suponiendo por simplicidad el caso discreto) se puede escribir de la forma

(1.1)

donde, en la llamada notación de Dirac, los son operadores proyectores sobre el subespacio  de dimensión uno (rectas) generado por el vector  (Hughes 1989, 64). El conjunto de los forman una base ortonormal del espacio de Hilbert (Ballentine 1990, 9: Sakurai 1994 18-19), y cada vector es llamado autovector de . Por otro lado, el conjunto es un conjunto de números reales (parametrizados discretamente por el índice ) llamado espectro de , y cada valor  es llamado autovalor de (Hughes 1989, 42-43; Ballentine 1990, 8; Sakurai 1994, 17-19). A veces también se menciona a los  como autoproyectores de . Como el conjunto de los  son ortonormales, los autoproyectores  correspondientes resultan ser ortogonales: esto significa que , donde el símbolo es igual a 1 si , y es 0 en caso contrario.

Haciendo uso de la expresión de (1.1), es muy fácil ver que (Sakurai 1994, 17). Así decimos que la magnitud toma valor  sobre el subespacio  generado por  porque al aplicar sobre , nos devuelve simplemente el valor  multiplicado por . Así, los distintos valores  que participan en la descomposición espectral son los posibles valores que puede tomar la magnitud , los cuales pueden ser corroborados en una medición de dicha magnitud (Hughes 1989, 64). Lo central aquí es que cada posible valor de queda naturalmente asociado al subespacio  y, por lo tanto, al proyector  que proyecta sobre . Debido a esta asociación, las propiedades que asignan un valor, o rango de valores, a la magnitud pueden ser representadas por el proyector asociado a ese valor, o rango de valores. Por ejemplo, la propiedad " con valor igual a 5” se podrá representar por el proyector . En cambio, la propiedad " con valor mayor o igual a 5 y menor o igual que 7”, se representará por el proyector . Como hemos dicho, cada proyector se corresponde con un subespacio en el espacio de Hilbert, por lo que también podemos representar cada propiedad como un subespacio. Esto es de hecho lo que en general se hace en la bibliografía. Aquí, sin embargo, orientados a lo que el formalismo de historias cuánticas necesita, buscaremos tratar las propiedades principalmente en términos de proyectores.

Entre las distintas propiedades que pueden predicarse, existen dos muy particulares: la propiedad universal, también llamada identidad , que siempre podrá asignarse al sistema; y la propiedad nula, también llamada cero , que nunca podrá asignarse al sistema. Identificaremos la propiedad universal  con el proyector identidad en el espacio de Hilbert del sistema, que es el operador que, aplicado a cualquier vector, lo deja idéntico. Es muy útil representar este operador por la suma de todos los posibles autoproyectores asociados a una magnitud dada, es decir  (Ballentine 1990, 10; Sakurai 1994, 19). Sin embargo esa representación no es única; volveremos a esta cuestión más abajo, con la importante noción de espacio muestral. Por otro lado, la propiedad nula se podrá representar por el proyector nulo del espacio de Hilbert del sistema, es decir por el  visto como operador, que transforma cualquier vector en  el vector nulo (Hughes 1989, 15).

Dentro del espacio de Hilbert se pueden definir tres operaciones básicas entre subespacios, que dan como resultado otro subespacio: la intersección, la suma, y el complemento ortogonal de subespacios (Hughes 1989, 190-191; Vanni y Laura 2008; Vanni 2010). Con el conjunto de todos los subespacios del espacio de Hilbert y estas operaciones, queda definida una estructura de propiedades cuánticas, la cual en este caso no resulta booleana (Mittelstaedt 1978, 27; Hughes 1989, 201-206; Bub 1997, 22-30; Vanni 2010).

Como en el caso clásico, es posible identificar clases de propiedades lógicamente equivalentes con proposiciones, y así derivar de la estructura de propiedades una estructura lógica, donde los conectivos conjunción , disyunción , y negación  se corresponden ahora con las operaciones de intersección, suma, y complemento ortogonal, respectivamente. El álgebra de la estructura lógica cuántica resulta no ser booleana. Adicionalmente, no es posible representar una relación de inferencia lógica asociada a la inclusión de subespacios, como uno esperaría de su análogo clásico: debido a la pérdida de características booleanas, en el caso cuántico no es posible definir una implicación compatible con una asignación de verdad consistente (Hughes 1989, 206; Omnès 1994, 185). Bajo esta limitación, muchas veces las inferencias en mecánica cuántica son elaboradas en función de probabilidades extremas 0 o 1 (Omnès 1994, 157, Omnès 1998, 142).

Como estamos interesados en representar a las propiedades en términos de proyectores y no en términos de sus correspondientes subespacios, debemos encontrar qué operaciones entre proyectores corresponden a las operaciones lógicas mencionadas. Antes de proseguir, sin embargo, es necesaria una aclaración respecto de las operaciones posibles entre propiedades incompatibles. En mecánica cuántica, dos magnitudes y  se dicen incompatibles si sus correspondientes operadores no conmutan, esto es, si su conmutador no es nulo (Sakurai 1994, 29). El conmutador entre y se define como . Si dos magnitudes son incompatibles, cumplen una relación de incerteza y, por consiguiente no es posible predicar sus propiedades de valor de modo simultáneo, es decir, como conjunciones (Ballentine 1990, 183; Sakurai 1994, 35). La postura tradicional consiste en sostener que las conjunciones tienen sentido sólo si corresponden a magnitudes compatibles. Esta es la postura adoptada en el formalismo de historias, sosteniendo además que no sólo las conjunciones, sino también las disyunciones tienen sentido sólo si corresponden a magnitudes compatibles. (Griffiths 1998, 1609; Griffiths y Omnès 1999, 28; Griffiths 2003, 1426). Otra postura sin embargo es la de la llamada lógica cuántica (Birkhoff y von Neumann 1936), que considera todas las operaciones bien definidas aun cuando las magnitudes asociadas sean incompatibles. En este caso, la expresión para estas operaciones en términos de proyectores, en particular para la intersección y la suma de subespacios, no es trivial (Mittelstaedt 1978, 20-21; Vanni 2010, 45).

Sin embargo, cuando se trata de la conjunción, disyunción, y negación  de propiedades de valor de magnitudes compatibles, entonces las operaciones entre los correspondientes proyectores pueden definirse fácilmente. El operador de la conjunción es simplemente el producto de los operadores, es decir:

(1.2)

El operador de la disyunción, por otro lado, es la suma de los operadores menos el de la intercesión:

(1.3)

Y finalmente, el de la negación es:

(1.4)

Si y  son además ortogonales, se tiene , expresión ésta que justifica por qué la propiedad mencionada más arriba tiene el proyector indicado (Vanni 2010).

Dos nociones muy importantes en el formalismo de historias cuánticas son la noción de espacio muestral (Griffiths 1996, 2760;  1998, 1605) y, asociada a la anterior, la noción de contexto (Vanni, 2010, 48; Laura y Vanni 2010). Diremos que un particular espacio muestral asociado a una magnitud es el conjunto de propiedades que queda determinado por una partición completa en subconjuntos disjuntos de su espectro. En forma más clara, si es una magnitud representada por un operador en un espacio de Hilbert de dimensión  y su espectro viene dado por , entonces una partición con el requerimiento mencionado será por ejemplo , , , . De esta manera, el espacio muestral asociado a la magnitud , con esa partición, quedará determinado por el conjunto de propiedades representadas por los proyectores de la forma . La partición es disjunta porque cada  tiene intersección nula con los restantes, y es completa porque la unión de todos los  constituyen el espectro completo de . Esto resulta en el hecho de que los  representen propiedades de valor, o rango de valores de , que son excluyentes y exhaustivas; por consiguiente, dichos  serán ortogonales, , y además sumarán la identidad del espacio de Hilbert del sistema . Se dice que los  que cumplen estas dos últimas propiedades forman una descomposición proyectiva de la identidad asociada a la magnitud . Hacemos notar que los  no son necesariamente autoproyectores de, porque no necesariamente representan propiedades de valor único. Son suma de subconjuntos disjuntos de autoproyectores de . Sólo en el caso particular de tener la partición más refinada posible del espectro de , dada por , tendremos que . En ese caso, los  son iguales a los autoproyectores de , y así  es la descomposición habitual de la identidad en términos de los autoproyectores de . Otra cosa que es importante subrayar es que los proyectores que determinan una descomposición proyectiva conmutan entre sí; por lo tanto, representan propiedades cuánticas compatibles.

Un contexto, por otro lado, es el conjunto de todas las propiedades formadas