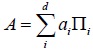Historias en mecánica cuántica
Leonardo Vanni
Universidad de Buenos Aires - Universidad Nacional de General Sarmiento
La premisa básica del formalismo de historias cuánticas consiste en abandonar la descripción de los sistemas cuánticos en términos de la evolución del estado, regida por la ecuación de Schrödinger. Las evoluciones pasan a ser descriptas en términos de historias, las cuales son entendidas como secuencias estocásticas de propiedades a distintos tiempos. El logro del formalismo es que permite lidiar con las dificultades conceptuales que resultan de la estructura lógica de las propiedades cuánticas, que no respeta la estructura lógica clásica, y a la vez permite desprenderse de la peculiar relación que la interpretación ortodoxa establece entre la evolución del estado cuántico y la asignación de propiedades al sistema en consideración. Si bien el formalismo de historias no puede predecir qué historia se actualizará en el decurso de los eventos, puede determinar condiciones específicas que establecen el conjunto de historias posibles para las propiedades y tiempos considerados. Este conjunto es una suerte de “mapa" de las posibles evoluciones que puede desarrollar el sistema. Dichas evoluciones serán aquéllas que, con una fórmula de la probabilidad previamente definida, cumplan los axiomas de la probabilidad clásica. En términos lógicos, el conjunto de todas las historias posibles determina el universo de discurso del sistema, siendo cada historia considerada como una “proposición elemental de evolución”, es decir, la entidad mínima por medio de la cual es posible describir la dinámica del sistema.
En la presente entrada, en primer lugar presentaremos las bases mínimas necesarias para comprender los aspectos fundamentales de la estructura lógica de las propiedades cuánticas, y luego desarrollaremos dos versiones del formalismo de historias cuánticas: el de Historias Consistentes y el de Historias Contextuales.
Estructura de propiedades cuánticas ↑
La utilidad de cualquier teoría física consiste en su capacidad de describir las propiedades de los sistemas que estudia, operando con ellas en algún tipo de estructura lógica. Sólo así se podrá entender, explicar y predecir el comportamiento de esos sistemas. Para lograr esto, la teoría debe ser capaz de incorporar elementos formales capaces de representar dichas propiedades en un marco teórico específico.
Cuando hablamos de propiedades de un sistema, aquí nos estamos refiriendo a propiedades de valor que toman sus magnitudes. Por ejemplo, una magnitud fundamental de cualquier sistema físico es su energía E. Asignar una determinada “propiedad de valor” a la magnitud energía es asignar o establecer un valor, o rango de valores a su energía. Así, p5=“energía igual a 5 ergios”, p[5,7]=“energía entre 5 y 7 ergios”, son ejemplos de propiedades de valor un sistema físico.
La mecánica clásica y la mecánica cuántica poseen diferentes elementos formales, sujetos a diferentes estructuras algebraicas, para representar sus propiedades. Estas diferencias son la base sobre la cual radica gran parte de las dificultades conceptuales encontradas a la hora de compatibilizar ambas teorías. En la física clásica, las propiedades de valor de un sistema pueden representarse por subconjuntos o regiones en el llamado espacio de fases del sistema (Hughes 1989, 58). El estado, por otro lado, se representa con un punto en ese espacio. Una propiedad se verifica en el sistema si el estado, como punto, pertenece a la región que representa la propiedad. Esto determina una particular estructura de propiedades en términos de operaciones entre conjuntos.
En términos lógicos, cada propiedad, o más exactamente, cada clase de propiedades lógicamente equivalentes, se puede identificar con una proposición, la proposición que adjudica la propiedad al sistema (Hughes 1989, 182). Con esta identificación, podemos transformar la estructura de propiedades en una estructura lógica. En el caso clásico esto se logra definiendo los conectivos lógicos de conjunción ∧, disyunción ∨, y negación ¬ en términos de operaciones de intersección, unión y complemento entre conjuntos respectivamente (Hughes 1989, 181-182; Omnès 1999, 101; Vanni 2010, 36). La estructura lógica de propiedades así establecida responde a un algebra booleana, la cual es en esencia el álgebra que establece las operaciones entre conjuntos (Hughes 1989, 178-184; Bub 1997, 15-22; Boole 2009). En este tipo de estructura es posible además establecer una relación de implicación, de suma importancia para los razonamientos lógicos, que es compatible con la relación de inclusión entre conjuntos y permite una asignación de verdad consistente sobre la estructura lógica (Hughes 1989, 202; Omnès 1992, 347; Omnès 1994, 184-185; Bub 1997, 15-20). Sin embargo, esto último y muchas de las características booleanas de la estructura lógica clásica dejan de ser válidas en la mecánica cuántica. Para comprender este punto, es necesario explicar cómo se describen cuánticamente las magnitudes físicas y sus propiedades de valor.
En la mecánica cuántica, las magnitudes físicas se representan mediante operadores hermíticos que actúan sobre vectores en el llamado espacio de Hilbert H del sistema (Hughes 1989, 63-65; Ballentine 1990, 2-8; Sakurai 1994, 14-16). Aclaramos aquí que, aunque la magnitud no es el objeto que la representa en la teoría, en este caso un operador, en lo que sigue la identificaremos con el operador. Así diremos “magnitud A” y escribiremos el operador correspondiente.
Cada espacio de Hilbert H tiene subespacios, que son subconjuntos de H que contienen el vector nulo, y además son cerrados ante sumas y multiplicaciones por un escalar (Hughes 1989, 35). Podemos decir que, en mecánica cuántica, las magnitudes físicas toman valores sobre ciertos subespacios en el espacio de Hilbert del sistema. Esto se puede ver al considerar que, debido a la llamada descomposición espectral (Hughes 1989, 50; Ballentine 1990, 10-11), cualquier operador A hermítico en un espacio de Hilbert de dimensión igual a d (suponiendo por simplicidad el caso discreto) se puede escribir de la forma
donde, en la llamada notación de Dirac, los Πi=|ai⟩⟨ai| son operadores proyectores sobre el subespacio Si de dimensión uno (rectas) generado por el vector |ai⟩ (Hughes 1989, 64). El conjunto de los {|ai⟩} forman una base ortonormal del espacio de Hilbert (Ballentine 1990, 9: Sakurai 1994 18-19), y cada vector |ai⟩ es llamado autovector de A. Por otro lado, el conjunto {ai} es un conjunto de números reales (parametrizados discretamente por el índice i∈[l,d]) llamado espectro de A, y cada valor ai es llamado autovalor de A (Hughes 1989, 42-43; Ballentine 1990, 8; Sakurai 1994, 17-19). A veces también se menciona a los Πi=|ai⟩⟨ai| como autoproyectores de A. Como el conjunto de los {|ai⟩} son ortonormales, los autoproyectores Πi correspondientes resultan ser ortogonales: esto significa que ΠiΠi′ = δii′Πi, donde el símbolo δii′ es igual a 1 si i=i′, y es 0 en caso contrario.