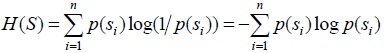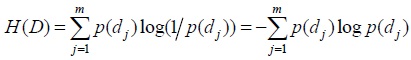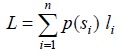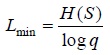La Teoría de la Información de Claude E. Shannon, es sin duda uno de los avances científicos más importantes del siglo XX. El principal objetivo de esta teoría es el de proporcionar una definición rigurosa de la noción de información que permita cuantificarla. Fue desarrollada con el objetivo de encontrar límites fundamentales en las operaciones de procesamiento de señales tales como compresión de datos, almacenamiento y comunicación. Sus aplicaciones se extienden a campos diversos, entre ellos la física, la química, la biología, la inferencia estadística, la robótica, la criptografía, la computación, la lingüística, el reconocimiento de patrones y la teoría de la comunicación. En esta entrada discutimos los aspectos centrales del formalismo de Shannon y algunos de sus problemas interpretacionales.
Contenido
- 1 Mundialización e información
- 2 El problema comunicacional y la noción de información
- 3 El problema de la codificación
- 4 Medidas de información
- 5 Los teoremas de Shannon
- 6 Distintas interpretaciones
- 7 Perspectivas a futuro: Información cuántica
- 8 Conclusiones
- 9 Bibliografía
- 10 Cómo Citar
- 11 Derechos de autor
1 Mundialización e información ↑
El mundo que habitamos hoy, con el incesante desarrollo tecnológico, el aumento considerable de la población mundial y la creciente interacción entre individuos e instituciones de distintas regiones del planeta, ha dado lugar a un aumento sin precedentes en las capacidades de la especie humana para transmitir y procesar información. El ejemplo más conspicuo de esto es quizá el advenimiento de internet, una inmensa red que interconecta a miles de millones de personas en todo el planeta. Esta capacidad para transmitir y procesar información había tenido sus antecesores en el telégrafo, las ondas de radio, el teléfono y otros sistemas de comunicación más antiguos.
Algunos autores, han llegado a afirmar que vivimos en la ‘era de la información’. Independientemente del debate acerca de si esta caracterización histórica es adecuada o no, lo cierto es que el estudio de los problemas técnicos asociados a la transmisión, medición y procesamiento de la información ha cobrado vital importancia para las relaciones sociales y comerciales de la sociedad globalizada. Sin ir más lejos, los mercados actuales dependen fuertemente de que los canales informacionales entre los distintos agentes económicos funcionen en forma fluida y eficiente. Pero la importancia del estudio de los flujos informacionales y su correcto funcionamiento va más allá de la esfera estrictamente económica y abarca fines militares, científicos y recreativos.
En este contexto, el estudio de la Teoría de la Información ha tenido un creciente desarrollo, en el que cada vez más investigadores aúnan esfuerzos para resolver los desafíos planteados por la existencia de unos volúmenes de flujo de información muy difíciles de manejar y administrar. Y es especialmente importante que estos desarrollos contemplen el aspecto matemático formal de la noción de información, de forma tal que ésta se pueda medir y cuantificar para ser aplicada con fines tecnológicos. El desarrollo de una teoría matemática de la información, que permita describir adecuadamente los problemas que los ingenieros comunicacionales encuentran en su trabajo diario es el objetivo que persiguió Claude Shannon cuando desarrolló su formalismo.
Los conceptos y aspectos formales del edificio teórico creado por Shannon siguen siendo explotados y desarrollados en la actualidad. Es por ello que su estudio es de vital importancia para entender el estado actual de la Teoría de la Información, y sus posibles generalizaciones en términos de las florecientes Teorías de la Información Cuántica y de la Computación Cuántica (Duwell 2003; Duwell 2008; Caves y Fuchs 1996; Caves, Fuchs y Schack 2002b; Deutsch y Hayden 2000; Holik, Bosyk y Bellomo 2015; Jozsa 1998; Jozsa 2004; Schumacher 1995; Bub 2005; Clifton; Bub; Halvorson 2003; Nielsen; Chuang 2010; Hayashi 2006).
2 El problema comunicacional y la noción de información ↑
En su artículo ‘A mathematical theory of communication’ (Shannon 1948), Shannon introdujo los lineamientos fundamentales sobre los que se construiría posteriormente la Teoría de la Información. Algunos elementos preliminares de esta teoría habían sido discutidos previamente en la literatura (ver por ejemplo Hartley 1928, Nyquist 1924 y Nyquist 1928). En efecto, al comienzo de su artículo, Shannon señala que:
“El desarrollo de varios métodos de modulación, tales como PCM y PPM que intercambian ancho de banda para una tasa de señal a ruido ha intensificado el interés en una teoría general de la comunicación. Una base para esta teoría está contenida en los importantes artículos de Nyquist y Hartley en este tema. En el presente artículo extenderemos la teoría para incluir un número de nuevos factores, en particular el efecto del ruido en el canal, y los cambios posibles debido a la estructura estadística del mensaje original y debido a la naturaleza final de la destinación de la información.” (Shannon 1948)
Uno de los principales aportes de Shannon fue el especificar cuál es el problema informacional, y separar los aspectos formales de los aspectos semánticos asociados con el contenido del mensaje:
“El problema fundamental de la comunicación es el de reproducir en un punto exacta o aproximadamente un mensaje seleccionado en otro punto. Frecuentemente los mensajes tienen significado; esto es, ellos refieren o están correlacionados de acuerdo a algún sistema con ciertas entidades físicas o conceptuales. Estos aspectos semánticos de la comunicación son irrelevantes para el problema de ingeniería. El aspecto significativo es que el mensaje de hecho es uno seleccionado a partir de un conjunto de posibles mensajes. El sistema debe ser diseñado para operar para cada posible selección, no sólo para aquella que será seleccionada de hecho, dado que es desconocida al momento del diseño.” (Shannon 1948)
De este modo, Shannon define el problema en términos técnicos precisos, separando el problema de ingeniería concreto asociado al proceso de comunicación con los aspectos semánticos de la noción de información vinculados a su uso generalizado en el lenguaje cotidiano. Esto no significa que estos últimos desaparezcan o que no sean importantes; de hecho, los aspectos filosóficos de la Teoría de la Información han dado lugar a importantes debates en la literatura (ver por ejemplo Adriaans 2013; Adriaans y van Benthem, eds. 2008; Bar-Hillel 1964; Bar-Hillel y Carnap 1953; Lombardi 2005; Nauta 1972). Lo que señala Shannon es simplemente que los aspectos semánticos son irrelevantes para el problema planteado en la ingeniería del proceso comunicacional.
El formalismo de Shannon ha sido desarrollado desde diversos enfoques, que poseen un mayor o menor grado de abstracción (ver por ejemplo: Shannon 1943; Shannon 1948; Shannon y Weaver 1949; Cover y Thomas 1991; Khinchin 1957; Reza 1961; Bell 1957). Desde el punto de vista del abordaje Bayesiano a las probabilidades (Cox 1948; Cox 1961), es posible encontrar la medida de Shannon desde una perspectiva alternativa (ver por ejemplo Knuth 2004; Knuth 2005a; Knuth 2005b; Knuth 2012; Goyal y Knuth 2011). Este último enfoque se puede extender a modelos probabilísticos más generales, incluyendo la teoría cuántica y la entropía de von Neumann (Holik, Sáenz, y Plastino 2014; Holik, Plastino, y Sáenz 2016).
Antes de continuar, es importante destacar también que, aparte de la entropía de Shannon, existen otras medidas de la información, como por ejemplo la de Chaitin (1987), la de Fisher (Fisher 1925), y las entropías de Tsallis y Rényi (Rényi 1961; Tsallis 1988; Rastegin 2014; Holik, Bosyk, y Bellomo 2015) que no discutiremos aquí por razones de espacio. Sólo nos limitaremos a decir que estas medidas encuentran numerosas aplicaciones en diferentes contextos, y que tienen una relevancia similar a la de Shannon.
3 El problema de la codificación ↑
Shannon estableció resultados matemáticos acerca de los recursos que se necesitan para la codificación óptima y para la comunicación libre de errores. Estos resultados tuvieron aplicaciones en diversos campos ligados a la teoría de las comunicaciones, como en la radio, la televisión y la telefonía. Hoy en día se siguen aplicando en diversas disciplinas.
De acuerdo a Shannon (1948) (ver también Shannon y Weaver 1949), un sistema de comunicación general consta de varias partes. Una fuente, la cual genera un mensaje a ser recibido en el destinatario. Un transmisor, que transforma el mensaje generado en la fuente en una señal a ser transmitida. En los casos en los que la información es codificada, el proceso de codificación también es implementado por el transmisor. Un canal es cualquier medio que sirva para que la señal se transmita desde el transmisor al receptor. Este puede ser, por ejemplo, un cable, una fibra óptica o una señal inalámbrica. Un receptor, que reconstruye el mensaje a partir de la señal, y finalmente, un destinatario, que es quien recibe el mensaje. En el siguiente dibujo se representan estos elementos en forma esquemática:
La fuente S es un sistema que contiene un conjunto de estados diferentes s1,...,sn, llamados usualmente letras. Un aspecto central de la teoría de Shanonn es que es posible asignar probabilidades de ocurrencia para los distintos estados de la fuente. Es decir, los estados s1,...,sn son producidos con probabilidades p(s1),...,p(sn). Notar que estas distribuciones de probabilidad pueden ser modeladas usando los axiomas de Kolmogorov (Kolmogorov 1933). La cantidad de información generada por la fuente debido a la ocurrencia del estado si se define como:
Dado que S produce sucesiones de estados (estas sucesiones son usualmente llamadas mensajes), la entropía de la fuente S se define como la cantidad promedio de información producida por la fuente:
En forma análoga, el destinatario D es un sistema con un rango de estados posibles d1,...,dm, a los cuales se le asignan probabilidades p(d1),...,p(dm). La cantidad de información I(dj) recibida en el destinatario debido a la ocurrencia de dj se define como:
Y la entropía del destinatario se define como la cantidad promedio de información recibida:
4 Medidas de información ↑
En su artículo original, Shannon (1948, 349) discute la conveniencia del uso de una función logarítmica en la definición de entropías:
“Si el número de mensajes en el conjunto es finito, este número o cualquier función monótona de él puede ser considerado como una medida de la información producida cuando se elije un mensaje del conjunto, siendo todas las opciones igualmente probables. Como fue subrayado por Hartley, la elección más natural es la función logarítmica. Aunque esta definición debe ser generalizada considerablemente cuando consideramos la influencia de la estadística del mensaje y cuando tenemos un rango continuo de mensajes, en todos los casos vamos a usar una medida esencialmente logarítmica.” (Shannon 1948)
Shannon continúa diciendo que esta definición encuentra muchos usos prácticos, dado que muchos parámetros importantes en ingeniería varían linealmente con el logaritmo del número de posibilidades. Señala que es al mismo tiempo una medida intuitiva, porque es usual medir magnitudes comparando linealmente con unidades de medida. Además de estas ventajas, es matemáticamente adecuada dado que resulta ser que muchas operaciones llevadas a cabo con el logaritmo se vuelven mucho más simples que en términos de otras formas funcionales.
La elección de una base logarítmica se corresponderá con la elección de una unidad de medida de la información. Si la base usada es 2, la unidad resultante se llamará ‘bit’. Este término proviene de la contracción del término en inglés ‘bynary digit’. Con estas definiciones, un bit terminará siendo la cantidad de información que se obtiene cuando una de dos alternativas igualmente probables es especificada. En otras palabras, una fuente S con dos estados que puede adoptar los valores 1 y 2 con la misma probabilidad, tendrá una cantidad de información de un bit. Otras bases dan lugar a diferentes unidades de la información. Por ejemplo, si se usan logaritmos naturales, la unidad de medida en este caso será el nat (que es la contracción del término en inglés natural unit). Cuando se usa la base 10 de los logaritmos, la unidad se llama Hartley. La posibilidad de usar diferentes unidades para cuantificar la información muestra la diferencia entre la cantidad de información asociada a un evento y el número de símbolos binarios necesarios para codificarlo. Es importante mencionar que el “bit” es una unidad de medida, y el hecho de que distintas unidades de medida puedan ser usadas no afecta a la naturaleza de la información.
De las definiciones es bastante claro que H(S) y H(D) son cantidades de información promedio. Sin embargo, en la literatura son llamadas usualmente entropías. Efectivamente, la forma funcional que poseen estas medidas de la información, es completamente análoga a las formas funcionales que la entropía adquiere en distintas teorías físicas. Esta terminología refleja una problemática profunda en los fundamentos de la teoría de la información. Esto es así a tal punto que el carácter intrigante de esta magnitud y sus propiedades se manifestó al comienzo de la formulación de la teoría. En efecto, de acuerdo a las palabras mismas de Shannon refiriéndose a cómo llamar a su nueva medida:
“Mi preocupación más grande era cómo llamarla. Pensé en llamarla ‘información’, pero esa palabra estaba muy usada, de forma tal que decidí llamarla ‘incerteza’. Cuando discutí el asunto con John von Neumann, el tuvo una idea mejor. Von Neumann me dijo: ‘Deberías llamarla entropía, por dos motivos. En primer lugar tu función de incerteza ha sido usada en la mecánica estadística bajo ese nombre, y por ello, ya tiene un nombre. En segundo lugar, y lo que es más importante, nadie sabe lo que es la entropía realmente, por ello, en un debate, siempre llevarás ventaja.’” (Tribus and McIrving 1971, 180).
La conexión con la física a la que hace mención von Neumann en la cita de arriba ha sido estudiada profundamente en la literatura física y filosófica (ver por ejemplo Landauer 1991; Landauer 1996; Lombardi 2005; Duwell 2003; Duwell 2008; Jozsa 1998; Jozsa 2004; Deutsch y Hayden 2000; Timpson 2003; Timpson 2004; Timpson 2006; Timpson 2008; Timpson 2013; Stonier 1990; Stonier 1996; Floridi 2010; Floridi 2011; Floridi 2013; Brukner y Zeilinger 2001; Brukner y Zeilinger 2009)
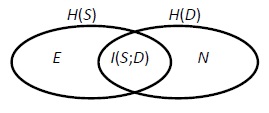
La relación entre las entropías de la fuente H(S) y del destinatario H(D) se puede representar intuitivamente por el siguiente diagrama:
Donde I(S;D) es la información mutua: la cantidad promedio de información generada en la fuente S y recibida en el destinatario D. E es la equivocación: la cantidad promedio de información generada en S pero no recibida en D. N es el ruido: la cantidad promedio de información recibida en D pero no generada en S. Como el diagrama sugiere desde un punto de vista intuitivo, la información mutua se define como:
La equivocación E y el ruido N son medidas de la independencia entre la fuente y el destinatario, dado que si S y D son completamente independientes, los valores de E y N son máximos (E = H(S) y N = H(D)), y el valor de I(S;D) es mínimo (I(S;D)=0). Por otro lado, si la dependencia entre S y D es máxima, los valores de E y N son mínimos (E = N = 0), y el valor de I(S;D) es máximo (I(S;D)=H(S)=H(D)).
Los valores de E y N son funciones no solo de la fuente y del destinatario, sino también del canal de comunicación CH. La introducción del canal de comunicación lleva directamente a la posibilidad de que se produzcan errores en el proceso de transmisión. El canal CH se puede definir como una matriz [p(dj|si)], donde p(dj|si) es la probabilidad condicional de ocurrencia de dj en el destinatario dado que si</sib> ocurrió en la fuente S. Los elementos de cada columna de [p(dj|si)] suman uno. De este modo, E y N se pueden expresar como:
donde ![]() . La capacidad del canal C se define como:
. La capacidad del canal C se define como:
Donde el máximo se toma sobre todas las posibles distribuciones ![]() en la fuente. La magnitud C se interpreta como la cantidad de información promedio más grande que puede ser transmitida por el canal de comunicación CH.
en la fuente. La magnitud C se interpreta como la cantidad de información promedio más grande que puede ser transmitida por el canal de comunicación CH.
5 Los teoremas de Shannon ↑
Los dos resultados más importantes que obtuvo Shannon son los teoremas conocidos como primer teorema de Shannon y segundo teorema de Shannon. De acuerdo al primer teorema, o teorema de codificación sin ruido, el valor de la entropía H(S) de la fuente es igual al número de símbolos necesarios en promedio para codificar una letra de la fuente usando un código ideal: H(S) mide la compresión óptima de los mensajes de la fuente. La prueba del teorema se basa en el hecho de que los mensajes de longitud N que produce S pueden ser clasificados en dos clases. Una de estas clases tiene aproximadamente 2NH(S) mensajes típicos. La otra clase, contiene los mensajes atípicos. Cuando N → ∞, la probabilidad de un mensaje atípico se vuelve despreciable. Por ello, se puede concebir a la fuente como produciendo sólo 2NH(S) mensajes posibles. Esto sugiere una estrategia natural para codificar: cada mensaje típico es codificado en una secuencia binaria de longitud NH(S), que es en general más corta que la longitud N del mensaje original.
En los años 40 se pensaba que el incremento de la tasa de transmisión de información sobre un canal de comunicación siempre aumentaría la probabilidad de error. El segundo teorema, conocido como teorema de codificación en un canal con ruido, sorprendió a la comunidad de la teoría de la comunicación probando que esa hipótesis no era cierta si se mantenía la tasa de comunicación por debajo de la capacidad del canal. La capacidad del canal es igual a la tasa máxima con la cual la información puede ser enviada por el canal y recuperada en el destinatario con una probabilidad de error despreciable.
Vamos a ver esto con un poco más de detalle. La fuente consiste en un sistema S de n estados si, que se pueden pensar como letras de un alfabeto As = {s1,...,sn}, cada una con su propia probabilidad p(si). Las secuencias de letras son llamadas mensajes. La entropía de la fuente H(S) se puede calcular exclusivamente en términos de estos elementos, y se mide en bits cuando el logaritmo tiene base 2. A su vez, el transmisor codifica el mensaje de la fuente y esto equivale a hacer una conversión entre el alfabeto de la fuente As = {s1,...,sn}, y el código del alfabeto del transmisor T, que viene dado por AC = {c1,...,cq}. Los elementos ci son llamados símbolos. La secuencia de símbolos producidos por el transmisor y que entran al canal se llama señal. El alfabeto de n símbolos AS puede variar mucho dependiendo de los distintos dispositivos empleados. Por otro lado, en muchos ejemplos de interés, conviene elegir un AC binario, es decir, con q = 2. En este caso, los símbolos son directamente dígitos binarios. Pero en el caso más general, el alfabeto del código se puede implementar físicamente por medio de sistemas que tengan una cantidad q de estados disponibles. Para el caso particular en que q = 2, los sistemas de dos niveles se pueden llamar cbits.
En el contexto de la teoría de la información de Shannon, codificar implica establecer un mapa entre las letras si del alfabeto de la fuente AS el conjunto de cadenas de longitud finita de símbolos del alfabeto del código AC. Estas suelen llamarse palabras-código. En general, las palabras-código no tienen la misma longitud. Cada palabra-código wi que corresponde a la letra si, va a tener una longitud li. Pero las longitudes li de las distintas palabras-código pueden variar. Es entonces útil definir una longitud de palabra-código promedio como:
L es entonces una medida de cuán compacto es el código. En otras, palabras, un código con un valor de L más pequeño será más eficiente, dado que en promedio, economiza más recursos informacionales para codificar los mensajes. El Teorema del Canal Sin ruido afirma que existe un proceso de codificación óptimo tal que la longitud de palabra-código promedio L está tan cerca como se quiera del límite inferior Lmin para L:
En la fórmula de arriba, si H(S) se mide en bits, log es el logaritmo en base 2.
Es importante enfatizar la diferencia entre el proceso de generación de la información en la fuente y la codificación de la información en el transmisor. La información generada en la fuente se mide con H(S), y sólo depende de las características de la fuente. Puede ser expresada en bits o en cualquier otra medida de la información. Además, la información así generada puede ser codificada mediante un alfabeto código de un número arbitrario de símbolos y la longitud promedio de las palabras código depende esencialmente de ese número.
Es importante mencionar que algunos autores, definen la noción de información en términos de los teoremas de Shannon. Timpson sostiene que “los teoremas de codificación que introdujeron los conceptos clásicos (Shannon 1948) y cuánticos (Schumacher 1995) de informaciónt [el concepto técnico de información] no sólo definen meramente medidas de estas cantidades. También introducen el concepto de qué es aquello que es transmitido, qué es aquello que es medido.” (Timpson 2008, 23). Desde esta perspectiva, el significado de la entropía H(S) queda definido por el primer teorema de Shannon: “preguntar cuánta información produce una fuente es preguntar hasta qué grado es compresible la salida de la fuente?” (Timpson 2008, 27). También: “La información de Shannon H(X) […] mide en qué medida se pueden comprimir los mensajes de la fuente.” (Timpson 2006, 592). En forma análoga, el Segundo teorema de Shannon es usado para explicar la información mutua H(S;D): “La interpretación más importante de la información mutua deriva del teorema de codificación ruidoso.” (Timpson 2004, 19). Es importante remarcar que, si bien la estrategia de definir la información de Shannon usando los teoremas de codificación lleva ciertamente a una perspectiva interesante, algunos autores la han criticado (ver por ejemplo Lombardi, Holik, y Vanni 2015).
6 Distintas interpretaciones ↑
No existe consenso en la literatura acerca de cómo interpretar la noción de información de Shannon. Algunos autores sostienen que ésta magnitud no representa a ninguna magnitud física. Uno de los principales defensores de esta postura es C. Timpson, quien afirma que la noción de información es un sustantivo abstracto (Timpson 2004, 2008, 2013). Debido a esto, concluye que “no sirve para referir a una cosa material o sustancia.” (Timpson 2004, 20). Esta concepción de la información está en consonancia con entender a H(S), no como una magnitud que cuantifica algo producido por la fuente S, sino como una medida de la compresibilidad de los mensajes.
Independientemente de las razones para llegar a la conclusión acerca de la naturaleza abstracta de la noción de información, es importante señalar que el hecho de que un ítem sea abstracto, no implica que no sea físico. No es necesario ser una substancia, ni una cosa concreta o una entidad material, para que un concepto sea físico. Basta para ello recordar que las teorías físicas están plagadas de propiedades, que representan observables físicos, que no son substancias de ningún tipo. Un ejemplo paradigmático de esto es el concepto de energía, que, a pesar de su inmaterialidad (al menos desde el punto de vista de algunas interpretaciones de este concepto), sigue jugando un rol fundamental en la mayoría de las teorías físicas de interés. En otras palabras, el hecho de que la información sea abstracta, no implica que no pueda ser considerada una magnitud física.
Una de las interpretaciones más comunes de la noción de información es la que se da en términos de conocimiento. En efecto, en muchas de sus aplicaciones la información provee conocimiento y modifica el estado de aquellos que la reciben. Naturalmente, es muy razonable argumentar que el vínculo entre la noción de información y el conocimiento pertenece a la esfera de nuestro uso cotidiano de la noción de información, el cual poco tiene que ver con el concepto de Shannon (ver Timpson 2004, 2013). Pero esta interpretación es quizá demasiado fuerte, y algunos enfoques indican lo contrario. Por ejemplo, Fred Dretske afirma que: “la información es una mercancía que, dado el receptor correcto, es capaz de entregar conocimiento.” (Dretske 1981, 47). Y este tipo de interpretaciones es muy común en diversos campos, por ejemplo: Jon M. Dunn define a la información como “aquello que queda de conocimiento cuando uno deja de lado la creencia, la justificación y la verdad” (Dunn 2001, 423). Y esta concepción es muy importante en algunas discusiones físicas. En palabras de Zeilinger “tenemos conocimiento, es decir, información, de un objeto solo a través de la observación” (Zeilinger 1999, 633). En algunos textos de ingeniería tradicionales, se encuentran frases como: “la información se mide como una diferencia entre el estado de conocimiento del receptor antes y después de la comunicación de la información.” (Bell 1957, 7). En este sentido es muy importante tener en cuenta el abordaje Bayesiano en física (ver por ejemplo: von Toussaint 2011, Jaynes y Bretthorst 2003, y Jaynes 1957). Este abordaje se caracteriza por la aplicación de distintas herramientas de la interpretación Bayesiana de la teoría de las probabilidades al estudio de problemas físicos, y ha encontrado aplicaciones fructíferas en diversas ramas de la física (Skilling 1988). Desde el punto de vista conceptual, el rasgo más relevante de este abordaje es que -en su versión más radical- defiende una interpretación epistémica (subjetivista) de la noción de probabilidad y de información (esta perspectiva ha alcanzado una importancia considerable entre las interpretaciones de la mecánica cuántica, ver por ejemplo Caves, Fuchs y Schack 2002). En otras palabras, las probabilidades que aparecen en las distintas teorías físicas, son interpretadas como la ignorancia que posee un agente racional respecto a los resultados de posibles experimentos. Aunque desde la perspectiva epistémica la información no sea considerada como un ente físico, se asume en general, que la posibilidad de adquirir conocimiento sobre la fuente de información está fundada en los estados físicos que subyacen a la situación observacional o experimental. En palabras de Dreske: “Las probabilidades condicionales usadas para calcular ruido, equivocación, y cantidad de información transmitidas[…] están todas determinadas por relaciones basadas en leyes que existen entre la fuente y la señal. Las correlaciones son irrelevantes a menos que estas correlaciones sean un síntoma de conexiones governadas por leyes.” (Dretske 1981, 77).
Una interpretación completamente diferente es aquella que considera a la información como una magnitud física. Esta es sin duda la posición de muchos físicos en la actualidad, para los cuales la característica principal de la información consiste en su capacidad de ser generada en un punto del espacio físico y transmitida a otro punto. De manera análoga, ésta puede ser acumulada, almacenada y convertida de una forma a otra. Desde el punto de vista de esta perspectiva, el vínculo con el conocimiento no es un tema central. Esto se refleja en el hecho de que la manipulación de la información puede estar destinada a propósitos de control, en donde no hay ningún agente cognoscente involucrado.
Esta visión ‘física’ de la información está apoyada por la creencia fuertemente establecida de que la transmisión de información entre dos puntos del espacio físico necesariamente requiere una señal que transporte esa información. En otras palabras, un proceso físico que se propague de un punto a otro. Uno de los más importantes defensores de esta perspectiva es Rolf Landauer. Este autor afirma que: “la información no es una entidad abstracta desprovista de cuerpo. Está representada por un grabado en una tabla de piedra, un spin, una carga, un agujero en una tarjeta agujereada, una marca en un papel, o algún equivalente.” (1996, 188; ver también Landauer 1991). La necesidad de un mecanismo de transpórte físico de la señal suena natural a la luz de la idea genérica de que las influencias físicas solo pueden ser transferidas a través de interacciones. En esta base, la información es concebida por muchos físicos como una entidad física con el mismo estatus que, por ejemplo, la energía (Aczél y Daróczy 1975).
Como mencionamos arriba, la naturaleza abstracta de la información no nos fuerza a adoptar una posición en la que la información no pueda ser considerada como una noción física. Muchos conceptos físicos han sufrido cambios de forma tal que, a medida que crece su abstracción y generalización, dejan de estar atados a una teoría física particular y permean a la totalidad de la física. Tal es el caso de la energía: esta noción está presente en todas las teorías físicas importantes y no está atada a ninguna en particular. Tiene diferentes manifestaciones físicas en dominios diferentes. Tomando este ejemplo como punto de partida, es muy tentador el intentar hacer una afirmación similar para la noción de información. Desde el punto de vista de esta línea argumentativa, no parecen haber serios obstáculos para concebir a la noción de información como un concepto físico.
La lista de posibles interpretaciones de la noción de información expuesta arriba no es exhaustiva. Sería imposible cubrir todo el espectro en esta breve entrada. Pero la lista expuesta arriba nos muestra que hay, en efecto, distintas posibilidades. Y existen argumentos atractivos para cada una de ellas. Es quizá por esto que aún hoy, el debate continúa.
¿Cuál es el camino a seguir frente a semejante proliferación de interpretaciones? Desde un punto de vista filosófico, existe la tentación de afirmar que estamos frente a un caso de indeterminación metafísica: disponemos de una teoría o formalismo que describe muchos ejemplos físicos de interés, pero la evidencia empírica disponible no es suficiente para tomar una posición concluyente en favor de una u otra interpretación. Esta situación empeora si se toman en cuenta las aplicaciones diversas que tiene la teoría de Shannon en distintos campos de la ciencia. Pero entonces se plantea el problema de responder a la pregunta: ¿qué es la Teoría de la Información de Shannon? Ciertamente disponemos de una formulación de un cuerpo teórico que encuentra diversas aplicaciones, y que fue motivado por los problemas subyacentes a la teoría general de la comunicación. Pero con el correr de los tiempos, su dominio de aplicación trascendió el de la ingeniería de la comunicación y se extendió a otras disciplinas. Paralelamente, el formalismo de Shannon fue objeto de una matematización creciente, en la que sus nociones son expuestas con un grado cada vez mayor de abstracción y rigurosidad. Paradójicamente, este estado de las cosas, en el que proliferan las aplicaciones e interpretaciones, ofrece al mismo tiempo una posibilidad de resolución. Como veremos a continuación, si se adopta una concepción pluralista de la teoría de la información, es posible encontrar un marco teórico en el que las diferentes interpretaciones dejan de ser rivales, y se convierten en herramientas con distintos campos de aplicación.
Como ya hemos mencionado, en algunos textos tradicionales sobre la teoría de la información, la teoría de Shannon es usualmente introducida desde una perspectiva física y vinculada con distintas problemáticas asociadas a la ingeniería de la comunicación. Sin embargo, algunos desarrollos subsiguientes se orientaron en una dirección formal que pone el centro en el rigor matemático, transformando a la Teoría de la Información en una suerte de rama de las matemáticas. Los conceptos básicos son introducidos en términos de nociones tomadas de la teoría matemática de la probabilidad, como por ejemplo, variables aleatorias y distribuciones de probabilidad. Las nociones de fuente, canal y receptor van dejando lugar al edificio del formalismo matemático, vacío en principio de toda interpretación física, y son introducidas a posteriori como posibles ejemplos de aplicaciones. Esta perspectiva formal puede encontrarse por ejemplo, en los libros clásicos de Aleksandr Khinchin (1957) y Fazlollah Reza (1961). En ellos, la Teoría de la Información es considerada como una suerte de extensión de la teoría matemática de las probabilidades (que puede ser considerada a su vez como un caso especial de la teoría de la medida). Uno de los ejemplos más importantes de este abordaje es el de Thomas Cover y Joy Thomas en su libro Elements of Information Theory (1991). Los autores conciben a la teoría de la información desde un punto de vista general, como un formalismo que es susceptible de ser aplicado en campos muy diversos:
“La teoría de la información responde a dos cuestiones fundamentales en la teoría de la comunicación: cuál es la compresión de datos máxima [...] y cuál es la tasa máxima de transmisión de comunicación [...]. Por esta misma razón, algunos consideran a la teoría de la información como un subconjunto de la teoría de la comunicación. Argumentaremos que ésta es mucho más aún. En efecto, tiene contribuciones fundamentales para hacer en física estadística (termodinámica), ciencias de la computación (complejidad de Kolmogorov o complejidad algorítmica), inferencia estadística (navaja de Occam: ‘La explicación más simple es la mejor’) y probabilidad y estadística (tasas de error para testeo y estimación de hipótesis óptimo)” (Cover y Thomas 1991, 1).
Esta concepción de la teoría de la información como un formalismo matemático que encuentra aplicaciones en diversos campos, abre la puerta a una concepción pluralista de la noción de información. Veamos con un poco de detalle cómo funciona esta perspectiva. El primer paso es definir dos variables aleatorias discretas con alfabetos A y B, y funciones de probabilidad p(x) = Pr(X = x), con x ∈ A, y p(y) = Pr(Y = y), donde y ∈ B, respectivamente. En este caso nos restringimos a variables discretas por simplicidad, pero la presentación se puede extender en forma natural a variables continuas. Una vez definidas estas nociones matemáticas, las entropías de las variables X y Y, H(X) y H(Y) se definen en forma usual. De forma análoga se pueden definir otras funciones importantes, como la entropía conjunta H(X, Y):
H(X,Y)=∑x∈X,y∈Y p(x, y) log p(x, y),
en términos de las variables X e Y y de la probabilidad conjunta. También es posible definir las entropías condicionales H(X|Y) de X dado Y, y H(Y|X) de Y dado X, que se definen en términos de las probabilidades condicionales p(x|y) y p(y|x) respectivamente:
H(Y |X) =∑x∈X p(x)H(Y |X = x) = − ∑ x∈X p(x) ∑ y∈Y p(y|x) log p(y|x)=
=− ∑ x∈X, y∈Y p(x,y)logp(y|x)
Con este formalismo, es posible probar que la información mutua I(X;Y), que se interpreta como una medida de la dependencia mutua entre dos variables aleatoreas, puede expresarse en términos de las cantidades definidas arriba de distintas formas:
I(X;Y)= H(X) − H(X|Y) = H(Y ) − H(Y |X) = H(X) + H(Y ) − H(X,Y)
Es importante mencionar que estas construcciones matemáticas se pueden extender canónicamente al caso de más de dos variables aleatorias, dando lugar a funciones como la entropía H(X1,X2,...,Xn) de una colección de variables aleatorias, o a la entropía mutua condicional H(X1,X2,...,Xn|Y) de las variables aleatorias X1,X2,...,Xn dado Y.
Un aspecto interesante de este abordaje matemático a la teoría de la información es que muestra las profundas conexiones estructurales entre la teoría de la medida, la teoría matemática de la probabilidad y la teoría de la información. En este abordaje, no es necesario establecer ninguna conexión con magnitudes físicas o problemas de la teoría de la comunicación. Además, esta construcción deja entrever hasta qué punto la teoría de la información depende de la teoría de la probabilidad matemática (basada en la teoría de la medida) desarrollada por A. N.Kolmogorov (Kolmogorov 1933). Y esto es interesante, dado que del mismo modo, las probabilidades que surgen a raíz del estudio de estados cuánticos pueden considerarse como originadas en medidas no-conmutativas (Holik, Sáenz, y Plastino 2014). De este modo, la teoría de la información cuántica podría entenderse como una teoría de la información asociada a probabilidades no Kolmogorovianas (para una discusión completa de esta perspectiva consultar las siguientes referencias: Holik, Plastino, y Sáenz 2016, y Holik, Bosyk y Bellomo 2015). En este abordaje, la noción de contextualidad juega un rol fundamental: las medidas no Kolmogorovianas que aparecen en mecánica cuántica, se pueden considerar como asignaciones de probabilidad (o grados de creencia) de un agente racional que se enfrenta a una situación con diferentes contextos complementarios. Cuando el álgebra de eventos a la que es expuesto el agente racional deja de ser un álgebra de Boole (como ocurre en el caso de las probabilidades Kolmogorovianas y en el Teoría de Shannon), y se transforma en el retículo de eventos posibles de un sistema cuántico, la medida de información natural deja de ser la entropía de Shannon, y debe reemplazarse por la entropía de von Neumann (Holik, Plastino y Sáenz 2016).
Además, el abordaje matemático-formal a la teoría de la información abre nuevas perspectivas para elucidar sus problemas de interpretación. Por un lado, esta visión permite considerar a la teoría de la información en forma análoga a como se concibe la teoría matemática de la probabilidad: el hecho de tornarla un concepto formal, permite hacerla aplicable a una variedad de campos distintos. En otras palabras, el desarrollo del formalismo matemático facilita su propagación a diversos campos y la aplicación de la teoría a distintas disciplinas: dota a la teoría de la información de una generalidad que le permite constituirse como una poderosa herramienta para el desarrollo del método científico. Este hecho, que parece ser innegable en el estado actual de desarrollo de la disciplina, tiene una implicación muy profunda para sus problemas interpretacionales: separa a la teoría de la información del lenguaje de las ciencias fácticas y del lenguaje ordinario, a un punto tal que podría afirmarse que no posee contenido semántico. Desde esta perspectiva, el significado de la noción de información posee una dimensión meramente sintáctica. Esta dimensión sintáctica es la que le otorga la generalidad al concepto.
Desde esta perspectiva formal, hay una relación lógica entre un objeto matemático y sus diferentes interpretaciones, en la que cada una de ellas dota al término de un contenido referencial específico. A modo de ejemplo, puede tomarse la interpretación física de la información, que concibe a la información como una magnitud física (ver por ejemplo Landauer 1991 y Landauer 1996). Pero es muy importante destacar también que la teoría de la información de Shannon ha encontrado interesantes aplicaciones en campos muy diversos que se desarrollan intensamente en la actualidad, como por ejemplo, las que relacionan a la entropía de Shannon y la teoría de juegos (ver, por ejemplo, Cover y Thomas 1991, Capítulo 6) o aplicaciones de la entropía de Shannon en la inversión y en el mercado de acciones (Cover y Thomas 1991, Capítulo 15). Otro ejemplo relevante es el del estudio de sistemas biológicos (Segal 2015; Yockey, Platzman y Quastler 1956), en el que la teoría de la información encuentra aplicaciones a la teoría de la evolución (Adami 2012), a la biología molecular (Yockey 1992) y al estudio del comportamiento (Pfeifer 2006). Algunos autores han intentado incluso utilizar argumentos informacionales para explicar las peculiaridades de los seres vivos y el origen de la vida (Yockey 2005). La existencia de estas aplicaciones, tan diversas en un su contenido, muestra que la interpretación del formalismo no puede estar unívocamente determinada.
Estos ejemplos ilustran que probablemente, sea necesario adoptar una interpretación pluralista de la teoría de la información, en la que las diferentes perspectivas no son rivales, sino casos particulares de aplicaciones de un formalismo lógico-matemático general. Todas estas interpretaciones serían legítimas en la medida que su aplicación sea exitosa en algún dominio de la ciencia o de la tecnología. Con respecto a esta visión, es interesante tener en cuenta las palabras del propio Shannon, quien afirmaba que:
“La palabra ‘información’ ha sido dotada de diferentes significados por varios escritores en el campo general de la teoría de la información. [...] Es difícilmente esperable que un único concepto de información de cuenta satisfactoriamente de las numerosas aplicaciones posibles de este campo general.” (Shannon 1993, 180).
7 Perspectivas a futuro: Información cuántica ↑
El debate interpretacional que discutimos en el apartado anterior cobra un impulso renovado a la luz del advenimiento de la teoría de la información cuántica: la posibilidad de desarrollar dispositivos de comunicación y de computación en los cuales los componentes obedecen a las leyes de la teoría cuántica, abre novedosas posibilidades tecnológicas, tanto para el almacenamiento, como para la transmisión y el procesamiento de la información. Plantea al mismo tiempo, nuevos interrogantes vinculados a los fundamentos de la ciencias físicas y de la computación (ver por ejemplo: Duwell 2003; Duwell 2008; Caves y Fuchs 1996; Caves, Fuchs y Schack 2002b; Deutsch y Hayden 2000; Holik, Bosyk y Bellomo 2015; Jozsa 1998; Jozsa 2004; Schumacher 1995; Bub 2005; Clifton, Bub y Halvorson 2003; Nielsen y Chuang 2010; Hayashi 2006). Respecto de la discusión acerca de la relación entre la Computación Cuántica y el principio de Church-Turing (que no podemos tratar aquí por una cuestión de espacio), ver (Deutsch 1985).
Es posible encontrar versiones de muchos de los resultados de la toría de Shannon en el conexto no conmutativo de la mecánica cuántica. En especial, existe una versión cuántica del teorema de codificación de Shannon (Schumacher 1995), en el que la codificación se efectúa en términos de sistemas cuánticos de dos niveles, conocidos con el nombre de qubits (abreviación de quantum bit). Los qubits constituyen la unidad elemental de información cuántica. En este caso, la medida de información de Shannon, debe ser reemplazada por su versión no conmutativa: la entropía de (von Neumann, Holik, Plastino y Sáenz). En general, es posible considerar a la teoría de la información cuántica como una versión no conmutativa (o no Kolmogoroviana) de la teoría de la infomación Shanon: es decir, una teoría de la información en la que las medidas de probabilidad involucradas no obedecen a los axiomas de Kolmogorov (Holik, Bosyk y Bellomo 2015). Esto está vinculado con el principio de complementariedad y al carácter contextual de la teoría cuántica (Renes 2013). Estas características peculiares del formalismo cuántico, junto con la noción de entrelazamiento, permiten desarrollar protocolos de información que carecen de análogo clásico, tales como el superdense coding y la teleportación cuántica. El lector interesado en profundizar en estos temas puede consultar la obra clásica de (Nielsen y Chuang 2010).
El desarrollo de dispositivos de procesamiento de la información cada vez más pequeños y eficientes, tales como telefonos celulares y computadoras personales, se choca inevitablemente con las leyes fundamentales de la física cuando sus componentes alcanzan la escala atómica. Algunos autores se preguntaron rápidamente si esto representaría un problema. Sin embargo, los desarrollos realizados en las últimas décadas muestran que, muy por el contrario, las leyes de la mecánica cuántica permiten sorprendentes posibilidades. Un ejemplo de esto es el de la seguridad informática y el desarrollo de la criptografía cuántica. Esta disciplina se basa en el hecho de que no es posible observar a un sistema cuántico sin perturbarlo, para desarrollar protocolos de generación de llaves secretas extremadamente seguros (Nielsen y Chuang 2010). Otro ejemplo conspicuo de las capacidades que ofrece el procesamiento de la información cuántica es el de la posibilidad de desarrollar computadoras cuánticas. Uno de los primeros en señalar la importancia de desarrollar mecanismos de procesamiento de la información basados en la teoría cuántica fue R. P. Feynman en 1982 (ver Feynman 1982), pero es también importante tener en cuenta (Manin 1980). Feynman hizo la observación de que la simulación de la evolución dinámica de sistemas cuánticos podría requerir una potencia de cómputo exponencial, y a ese fin, propuso la construcción de computadoras basadas en las leyes de la mecánica cuántica. Estas ideas fueron desarrolladas por otros autores, y el problema de la construcción de computadoras cuánticas se ha convertido en un campo de investigación muy activo en la actualidad, arrojando resultados sorprendentes (Schor 2000).
Los problemas en computación se pueden dividir en dos grandes grupos. Por un lado, están aquellos que se pueden computar en tiempos razonablemente cortos y que consumen recursos que crecen como una funcion polinomial del largo de la entrada del problema a resolver. Por otro lado, se encuentran aquellos cuya complejidad hace que se requiera un tiempo extemadamente largo para realizar el cómputo, de forma tal que se vuelven inaplicables en la práctica. Para estos últimos, los recursos computacionales usualmente crecen exponencialmente como función del largo de la entrada. Es posible demostrar que existen algortimos que permiten resolver ciertos problemas con recursos polinomiales usando computadoras cuánticas, mientras que no existe o no se conoce una version polinomial para resolverlos con computadoras clásicas. Tal es el caso del algoritmo de factorización de numeros enteros de Peter Schor (Schor 1997). El problema de, dado un número entero, encontrar su factorización en terminos de números primeros es de antigua data, y su resolución se hace cada vez más compleja (en terminos computacionales) a medida que el tamaño del número dado aumenta. Esto se traduce en que todos los algoritmos clásicos conocidos en la actualidad consumen recursos computacionales exponenciales: esto quiere decir que el problema de factorizar un número entero muy grande puede tardar una cantidad de tiempo tan grande, que lo hace completamente inútil en la práctica. Este hecho es aprovechado en importantes protocolos de seguridad informática en la actualidad, tales como los que se utilizan en transacciones bancarias. Sin embargo, utilizando computadoras cuánticas, el algoritmo de Schor permitiría resolver este problema en un tiempo razonable, y de esta forma, vulnerar muchos protocolos de seguridad informática. Es importante hacer una aclaración: el hecho de que no se conozca ningún algoritmo clásico que permita resolver el problema de la factorización en tiempo polinomial, no implica que este tipo de algoritmos no existan. Sin embargo, es posible probar que existen algunos algoritmos cuánticos que superan a todo algoritmo clásico para ciertas tareas. Tal es el caso del algoritmo de Simon (Simon 1997).
La perspectivas abiertas por la posibilidad de la computación cuántica, si bien promisorias, enfrentan un problema importante: la construcción de computadoras cuánticas es un desafío que presenta dificultades técnicas complejas, y al día de hoy, sólo ha sido posible implementar en el laboratorio algunos algoritmos muy sensillos (Tame et al 2007). No es claro si es posible aumentar la escala de tamaño de estos dispositivos significativamente y, al mismo tiempo, mantener la efectividad de los algoritmos cuánticos. Sin embargo, muchos investigadores son optimistas respecto de esta posibilidad, dado que se han realizado importantes advances (Montanaro, A., (2016)). Es importante notar que algunas compañías afirman haber desarrollado computadoras cuánticas, pero muchos investigadores se mantienen escépticos acerca de la efectividad de sus resultados (Shin et al (2014).
Con el advenimiento de la Teoría de la Información Cuántica, algunos conceptos cambiaron su significado, al menos para algunos autores. En este contexto, el concepto de qubit (contracción del término en inglés ‘quantum bit’) se hizo central. Pero el qbit es muchas veces definido no como una unidad de medida de la información, sino como un sistema físico concreto, a saber, un sistema cuántico de dos niveles usado para codificar la información de la fuente. Con el afán de evitar confusiones sobre la noción de bit, es útil seguir la sugerencia de Caves, C. y Fuchs, C. (1996), quienes proponen el término ‘cbit’ para referirse a un sistema clásico de dos niveles usado para codificar información de Shannon, explotando la analogía con el sistema cuántico de dos niveles usado para codificar información cuántica.
Finalmente, es importante remarcar también que, el hecho de que sea posible formular principios fundamentales de la mecánica cuántica en términos puramente informacionales (ver por ejemplo, Clifton, Bub y Halvorson 2003 y Bub 2005), ha llevado a muchos autores a la idea de que es posible dar interpretaciones de la física y de la naturaleza en general basadas en la teoría de la información. A este respecto, ver por ver por ejemplo (Vedral 2010).
8 Conclusiones ↑
En esta entrada hemos dado una breve introducción a la teoría de la información de Shannon. Hemos señalado su importancia en diversas disciplinas científicas así como en numerosas aplicaciones tecnológicas, especialmente para la teoría general de la comunicación. Desde el punto de vista puramente formal, hemos señalado hasta qué punto la Teoría de Shannon puede ser concebida como un formalismo matemático útil para modelar distintos problemas en diversas áreas del conocimiento, indicando que probablemente no exista una interpretación única o privilegiada del formalismo. A pesar del importante grado de desarrollo que ha alcanzado el formalismo y sus espectaculares aplicaciones en diversas disciplinas, la teoría de Shannon es aún un campo activo de debate debido al problema de sus posibles interpretaciones y la discusión acerca de sus fundamentos. En la actualidad, es imposible no mencionar los relativamente recientes desarrollos en el campo de la Teoría de la Información Cuántica y la Computación Cuántica, que prometen un abanico de aplicaciones tecnológicas revolucionarias, y abren al mismo tiempo la puerta a novedosos interrogantes en la física y en las ciencias de la computación (así como en otras disciplinas). En este contexto, el estudio y debate en torno a los fundamentos de la Teoría de la Información de Shannon puede ser de gran ayuda para entender los problemas y los desafíos que plantean los posibles desarrollos tecnológicos basados en la teoría cuántica. En gran parte debido a esto, el formalismo de Shannon cobra una inusitada actualidad.
9 Bibliografía ↑
Aczél, J. y Darócsy, Z. 1975. On measures of information and their characterization. New York-San Francisco-London: Academic Press.
Adami, C. 2012. “The use of information theory in evolutionary biology”. Annals of the New York Academy of Sciences 1256: 49–65. doi: 10.1111/j.1749-6632.2011.06422.x
Adriaans, P. 2013. “Information.” En The Stanford Encyclopedia of Philosophy (Fall 2013 Edition), editado por E. N. Zalta URL = http://plato.stanford.edu/archives/fall2013/entries/information/
Adriaans, P. y van Benthem, J., eds. 2008. Handbook of Philosophy of Information. Amsterdam: Elsevier Science Publishers.
Bar-Hillel, Y. 1964. Language and Information: Selected Essays on Their Theory and Application. Reading, MA: Addison-Wesley.
Bar-Hillel, Y. y Carnap, R. 1953. “Semantic Information.” The British Journal for the Philosophy of Science 4: 147-157.
Barwise, J. y Seligman, J. 1997. Information Flow. The Logic of Distributed Systems. Cambridge Cambridge University Press.
Bell, D. 1957. Information Theory and its Engineering Applications. London: Pitman & Sons.
Brukner, Č. y Zeilinger, A. 2001. “Conceptual Inadequacy of the Shannon Information in Quantum Measurements.” Physical Review A 63: #022113.
Brukner, Č. y Zeilinger, A. 2009. “Information Invariance and Quantum Probabilities.” Foundations of Physics 39: 677-689.
Bub, J. 2005. “Quantum mechanics is about quantum information”. Found. Phys. 35: 541–560.
Caves, C. M. y Fuchs, C. A. 1996. “Quantum Information: How Much Information in a State Vector?” En The Dilemma of Einstein, Podolsky and Rosen - 60 Years Later. Annals of the Israel Physical Society, editado por A. Mann y M. Revzen, 12: 226-257 (see also quant-ph/9601025).
Caves, C. M., Fuchs, C. A., y Schack, R. 2002b. “Unknown Quantum States: The Quantum de Finetti Representation.” Journal of Mathematical Physics 43: 4537-4559.
Chaitin, G. 1987. Algorithmic Information Theory. New York: Cambridge University Press.
Clifton, R.; Bub, J. y Halvorson, H. 2003. “Characterizing quantum theory in terms of information-theoretic constraints”. Found. Phys. 33: 1561–1591.
Cover, T. y Thomas, J. A. 1991. Elements of Information Theory. New York: John Wiley & Sons.
Cox, R. T. 1946. “Probability, frequency and reasonable expectation”. American Journal of Physics 14(1).
Cox, R. T. 1961. The Algebra of Probable Inference. Baltimore, MD: The Johns Hopkins Press.
Deutsch, D. y Hayden, P. 2000. “Information Flow in Entangled Quantum Systems.” Proceedings of the Royal Society of London A 456: 1759-1774.
Deutsch, D., 1985. “Quantum theory, the Church-Turing principle and the universal quantum computer”. Proceedings of the Royal Society of London A 400: 97-117.
Dretske, F. 1981. Knowledge & the Flow of Information. Cambridge MA: MIT Press.
Dunn, J. M. 2001. “The Concept of Information and the Development of Modern Logic”. En Non-classical Approaches in the Transition from Traditional to Modern Logic, editado por W. Stelzner, 423-427. Berlin: de Gruyter.
Duwell, A. 2003. “Quantum Information Does Not Exist.” Studies in History and Philosophy of Modern Physics 34: 479-499.
Duwell, A. 2008. “Quantum Information Does Exist.” Studies in History and Philosophy of Modern Physics 39: 195-216.
Feynman, R. 1982. “Simulating physics with computers”. International Journal Of Theoretical Physics 21: 467-488.
Fisher, R. 1925. “Theory of Statistical Estimation.” Proceedings of the Cambridge Philosophical Society 22: 700-725.
Floridi, L. 2010. Information – A Very Short Introduction. Oxford: Oxford University Press.
Floridi, L. 2011. The Philosophy of Information. Oxford: Oxford University Press.
Floridi, L. 2013. “Semantic Conceptions of Information”. En The Stanford Encyclopedia of Philosophy (Spring 2013 Edition), editado por E. N. Zalta. URL = http://plato.stanford.edu/archives/spr2013/entries/information-semantic/
Goyal, P. y Knuth, K. 2011. “Quantum theory and probability theory: their relationship and origin in symmetry”. Symmetry 3(2):171–206.
Hartley, R. V. L. 1928. “Transmission of Information”. Bell SystemsTechnical Journal p. 535.
Hayashi, M. 2006. Quantum Information. Berlin-Heidelberg: Springer.
Holik, F., Sáenz, M. y Plastino, A. 2014. “A discussion on the origin of quantum probabilities”. Annals of Physics 340(1):293 – 310.
Holik, F., Plastino, A. y Sáenz, M. 2016. “Natural information measures in Cox' approach for contextual probabilistic theories”, a publicarse en Quantum Information & Computation.
Holik, F., Bosyk, G. y Bellomo, G. 2015. “Quantum Information as a Non-Kolmogorovian Generalization of Shannon’s Theory”. Entropy 17(11): 7349-7373; doi:10.3390/e17117349
Jaynes, E. T. y Bretthorst, G. L. 2003. Probability Theory: The Logic of Science. Cambridge: Cambridge University Press.
Jaynes, E. T. 1957. “Information Theory and Statistical Mechanics”. Phys. Rev. 106: 620.
Jozsa, R. 1998. “Entanglement and Quantum Computation”. En The Geometric Universe, editado por S. Huggett, L. Mason, K. P. Tod, S. T. Tsou y N. M. J. Woodhouse, 369-79. Oxford: Oxford University Press.
Jozsa, R. 2004. “Illustrating the Concept of Quantum Information.” IBM Journal of Research and Development 4: 79-85.
Khinchin, A. 1957. Mathematical Foundations of Information Theory. New York: Dover.
Knuth, K. 2004. “Deriving laws from ordering relations”. En Bayesian inference and maximum entropy methods in science and engineering, volumen 707 de AIP Conf. Proc., 204–235. Amer. Inst. Phys., Melville, NY.
Knuth, K. 2005a. “Lattice duality: The origin of probability and entropy”. Neurocomputing 67(0): 245 – 274.
Knuth, K. 2004. “Measuring questions: relevance and its relation to entropy”. En Bayesian inference and maximum entropy methods in science and engineering, volumen 735 de AIP Conf. Proc., 517–524. Amer. Inst. Phys., Melville, NY.
Knuth, K. 2005b. “Toward question-asking machines: The logic of questions and the inquiry calculus”. En Society for Artificial Intelligence and Statistics, editado por Robert G. Cowell y Zoubin Ghahramani, 174 – 180. (Disponible electrónicamente en http://www.gatsby.ucl.ac.uk/aistats/ ).
Knuth, K. 2012. “What is a question?” En Bayesian inference and maximum entropy methods in science and engineering, volumen 659 de AIP Conf. Proc., 227–242. Amer. Inst. Phys., Melville, NY, 2003. [29] Kevin H. Knuth and John Skilling. Foundations of inference. Axioms, 1(1):38–73.
Kolmogorov, A. N. 1933. Foundations of Probability Theory. Berlin: Julius Springer.
Landauer, R. 1991. “Information is Physical.” Physics Today 44: 23-29.
Landauer, R. 1996. “The Physical Nature of Information.” Physics Letters A 217: 188-193.
Lombardi, O. 2004. “What is Information?” Foundations of Science 9: 105-134.
Lombardi, O. 2005. “Dretske, Shannon’s Theory and the Interpretation of Information.” Synthese 144: 23-39.
Lombardi, O., Holik, F. y Vanni, L. 2015. “What is Shannon Information?” Synthese (DORDRECHT); Lugar: Berlin. DOI: 10.1007/s11229-015-0824-z
MacKay, D. 1969. Information, Mechanism and Meaning. Cambridge MA: MIT Press.
Manin, Y. 1980. Computable and Uncomputable (en Ruso). Moscow: Sovetskoye Radio.
Nauta, D. 1972. The Meaning of Information. The Hague: Mouton.
Nielsen, M.A. y Chuang, I.L. 2010. Quantum Computation and Quantum Information. Cambridge: Cambridge University Press.
Nyquist, H. 1924. “Certain Factors Affecting Telegraph Speed”. Bell System Technical Journal, p. 617.
Nyquist, H. 1928. “Certain Topics in Telegraph Transmission Theory”. AIEE Trans. 47: 617.
Montanaro, A. 2016. “Quantum algorithms: an overview”. npj Quantum Information 2: 15023; doi:10.1038/npjqi.2015.23.
Pfeifer, J. 2006. “The Use of Information Theory in Biology: Lessons from Social Insects”. Biological Theory 1(3): 317–330.
Rastegin, A. 2014. “Tests for quantum contextuality in terms of q-entropies”. Quantum Information And Computation 14: 0996–1013.
Rényi, A. 1961. On Measures of Entropy and Information. Berkeley: University of California Press.
Renes, J. 2013. “The physics of quantum information: complementarity, uncertainty and entanglement”. International Journal of Quantum Information 11: 1330002.
Reza, F. 1961. Introduction to Information Theory. New York: McGraw-Hill.
Schumacher, B. 1995. “Quantum Coding.” Physical Review A 51: 2738-2747.
Schor, P. 2000. “Introduction to quantum algorithms”. Proceedings of Symposia in Applied Mathematics.
Schor, P. 1997. “Polinomial-time algorithms for prime factorization and discrete logarithms on a quantum computer”. SIAM J. Computing 26: 1474-1483.
Segal, J. 2015. “The notion of information in biology, an appraisal”. BIO Web of Conferences 4: 00017.
Shannon, C. 1948. “A Mathematical Theory of Communication.” Bell System Technical Journal 27: 379-423.
Shannon, C. 1993. Collected Papers, editado por N. Sloane y A. Wyner. New York: IEEE Press.
Shannon, C. y Weaver, W. 1949. The Mathematical Theory of Communication. Urbana and Chicago: University of Illinois Press.
Shin, S., Smith, G., Smolin, J. y Vazirani, U. 2014. “How “Quantum” is the D-Wave Machine?” arXiv:1401.7087v2.
Simon, D. 1997. “On the power of quantum computation”. Siam J. Comput. 26, 5: 1474–1483.
Skilling, J., Ed. 1988. Maximum Entropy and Bayesian Methods. London: Springer.
Stonier, T. 1990. Information and the Internal Structure of the Universe: An Exploration into Information Physics. New York-London: Springer.
Stonier, T. 1996. “Information as a Basic Property of the Universe.” Biosystems 38: 135-140.
Tame, M.S., Prevedel, R., Paternostro, M. , Bo, P. , Kim, M.S. y Zeilinger, A. 2007. “Experimental Realization of Deutsch’s Algorithm in a One-Way Quantum Computer”. Physical Review Letters 98: 140501.
Timpson, C. 2003. “On a Supposed Conceptual Inadequacy of the Shannon Information in Quantum Mechanics.” Studies in History and Philosophy of Modern Physics 34: 441-68.
Timpson, C. 2004. Quantum Information Theory and the Foundations of Quantum Mechanics. PhD diss., University of Oxford (quant-ph/0412063).
Timpson, C. 2006. “The Grammar of Teleportation.” The British Journal for the Philosophy of Science 57: 587-621.
Timpson, C. 2008. “Philosophical Aspects of Quantum Information Theory.” En The Ashgate Companion to the New Philosophy of Physics, editado por Dean Rickles, 197-261. Aldershot: Ashgate Publishing. Los números de página fueron tomados de la version online: arXiv:quant-ph/0611187.
Timpson, C. 2013. Quantum Information Theory and the Foundations of Quantum Mechanics. Oxford: Oxford University Press.
Tribus, M. y Mc Irving, E. C. 1971. “Energy and Information.” Scientific American 225: 179-188.
Tsallis, C. 1988. “Possible generalization of boltzmanngibbs statistics”. Journal of Statistical Physics 52(1-2): 479–487.
Vedral, V. 2010. Decoding Reality: The Universe as Quantum Information. Oxford: Oxford University Press.
von Toussaint, U. 2011. “Bayesian inference in physics”. Reviews of Modern Physics 83: 943.
Yockey, P. 2005. Information theory, evolution, and the origin of life. Cambridge: Cambridge University Press.
Yockey, P. 1992. Information theory and molecular biology. Cambridge: Cambridge University Press.
Yockey, H., Platzman, R. y Quastler, H., Eds. 1956. Information Theory in Biology. New York-London-Paris-Los Angeles: Pergamon Press.
10 Cómo Citar ↑
Holik, Federico. 2016. "Teoría de la información de Claude E. Shannon". En Diccionario Interdisciplinar Austral, editado por Claudia E. Vanney, Ignacio Silva y Juan F. Franck. URL=http://dia.austral.edu.ar/Teoría_de_la_información_de_Claude_E._Shannon
11 Derechos de autor ↑
DERECHOS RESERVADOS Diccionario Interdisciplinar Austral © Instituto de Filosofía - Universidad Austral - Claudia E. Vanney - 2016.
ISSN: 2524-941X